Wie kann ein Graph durchsucht werden? Eine mögliche Methode: von einem Startknoten wird ein erster Nachbarknoten aufgesucht und weitere Nachfolgeknoten aufgesucht. Erst wenn man in der Sackgasse steckt, geht man zurück und untersucht Nachbarknoten. Man arbeitet sich zuerst in die Tiefe vor, man spricht von Tiefensuche.
Mit der Simulation kann ein Graph gezeichnet und nach der Festlegung von Start ⬤ und Ziel ⬤ die Tiefensuche schrittweise simuliert werden:
- Linksklick: neuer Ort (Knoten)
- Linksdrag und drop auf anderen Knoten: neue Strecke (Kante)
- je ein Linksklick auf bestehende Knoten: Zielort ⬤ → Startort ⬤ → normaler Knoten ⬤ festlegen
- 's': Start der Simulation
- 'n': neues Streckennetz anlegen
Die Erkundung eines Höhlensystems könnte mit der Tiefensuche angegangen werden. Geht es darum alle Malereien in den Höhlenräumen zu dokumentieren, so würde sich dieses Verfahren eignen. Denn es werden alle Höhlenräume (Knoten) besucht, aber nicht alle Gänge (Kanten) begangen.
Aufgabe
Übersetzen Sie das folgende Höhlensystem in einen Graphen und simulieren Sie die Suche der Höhlenräume.
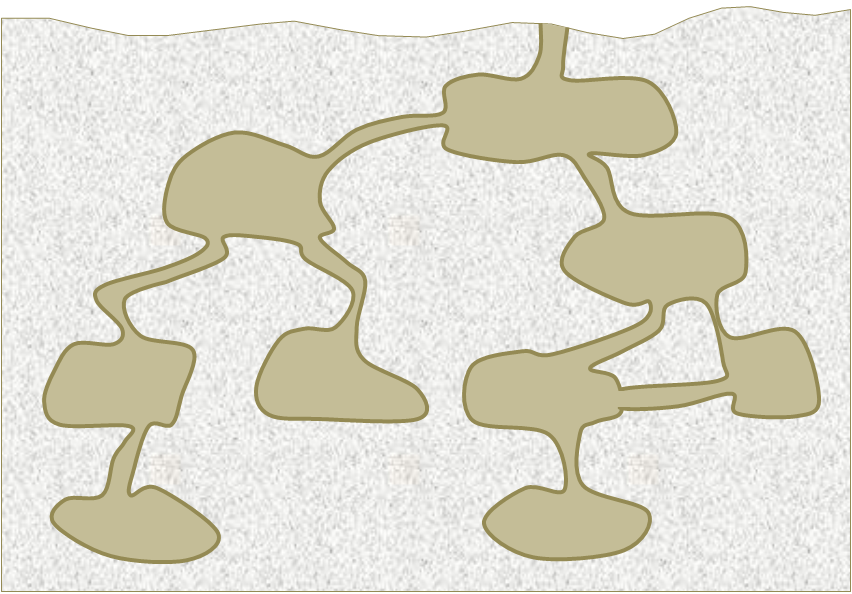
Lösungshinweise
Der Graph des Höhlensystems sieht wie folgt aus:
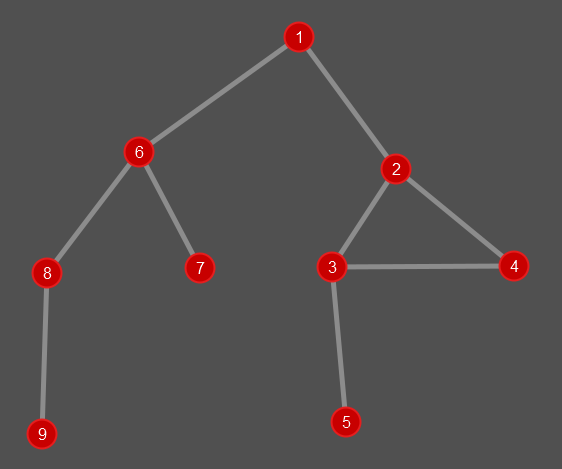
Die Simulation zeigt: alle Räume werden besucht und die Suche wird nicht im Dreieck 2, 3, 4 gefangen, da die besuchten Räume markiert werden. In der Realität könnten brennende Fackeln in den besuchten Räumen angebracht werden, welche in die Gänge leuchten.
Die Kante zwischen den Knoten 2 und 4 wird nicht begangen, ist jedoch durch die Fackeln der beiden Knoten ausgeleuchtet (hier gelb).
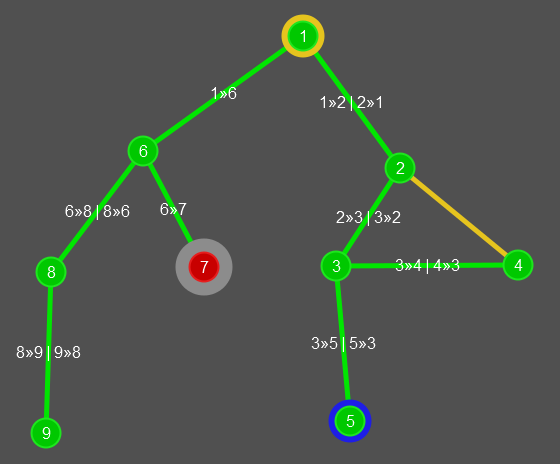
Eine zweite Suchmethode ist folgende:
von einem Startknoten werden zuerst alle noch nicht besuchten Nachbarknoten aufgesucht. Anschliessend wird nacheinander von jedem Nachbaknoten aus seine noch nicht besuchten Nachbarknoten besucht. Und so weiter, bis alle Knoten besucht sind. Man arbeitet sich in die Breite vor, entsprechend heisst das Verfahren Breitensuche.
Mit der Simulation kann ein Graph gezeichnet und nach der Festlegung von Start ⬤ und Ziel ⬤ die Breitensuche schrittweise simuliert werden:
- Linksklick: neuer Ort (Knoten)
- Linksdrag und drop auf anderen Knoten: neue Strecke (Kante)
- je ein Linksklick auf bestehende Knoten: Zielort ⬤ → Startort ⬤ → normaler Knoten ⬤ festlegen
- 's': Start der Simulation
- 'n': neues Streckennetz anlegen
Der Gang durch einen Irrgarten ist eine mögliche Anwendung.
Aufgabe
Übersetzen Sie den Irrgarten von Altjeßnitz (Sachsen-Anhalt, BRD) in einen Graphen und simulieren Sie ausgehend vom Start S die Suche nach dem Ziel Z.
Tipp: drucken Sie die untenstehende Grafik gross aus und zeichnen Sie darauf.
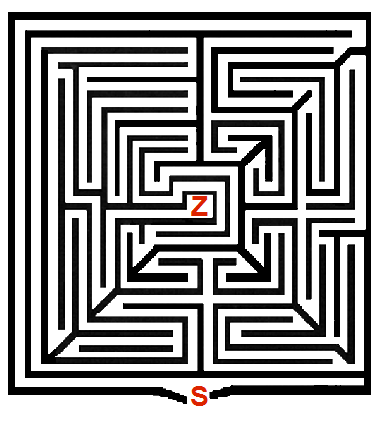
Lösung Schritt I
Als erstes werden alle Verzweigungen des Irrgartens als Knoten bezeichnet:
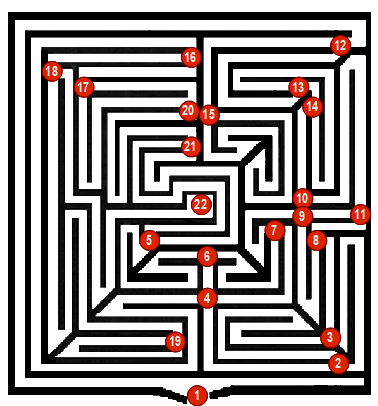
Nun werden alle Verbindungen zwischen den Knoten als Kanten eingefügt und das Geflecht entwirrt:
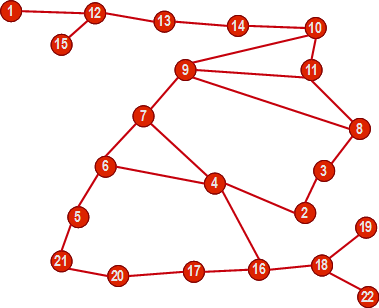
Lösung Schritt II
Nun kann der Graph in die Simulation übertragen werden:
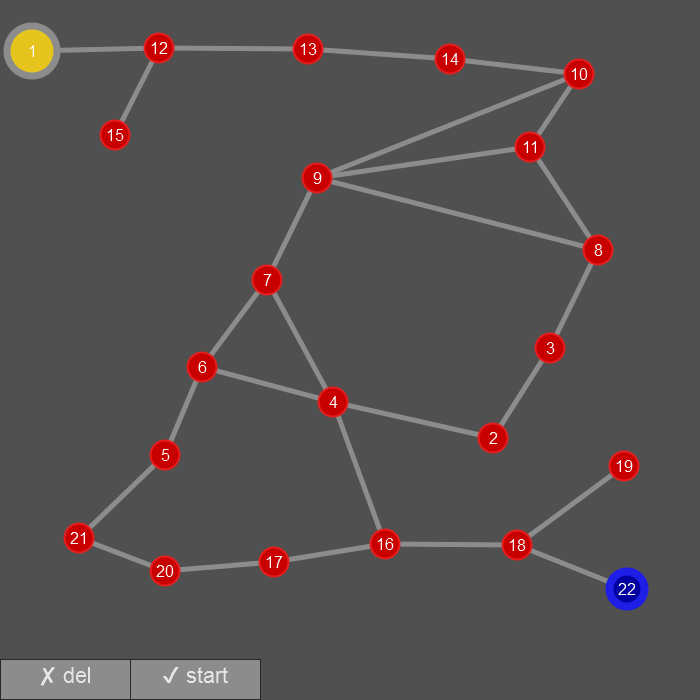
Die Simulation der Breitensuche zeigt, ein Irrgarten kann mit dieser Methode erfolgreich durchsucht. Man erreicht das Ziel.
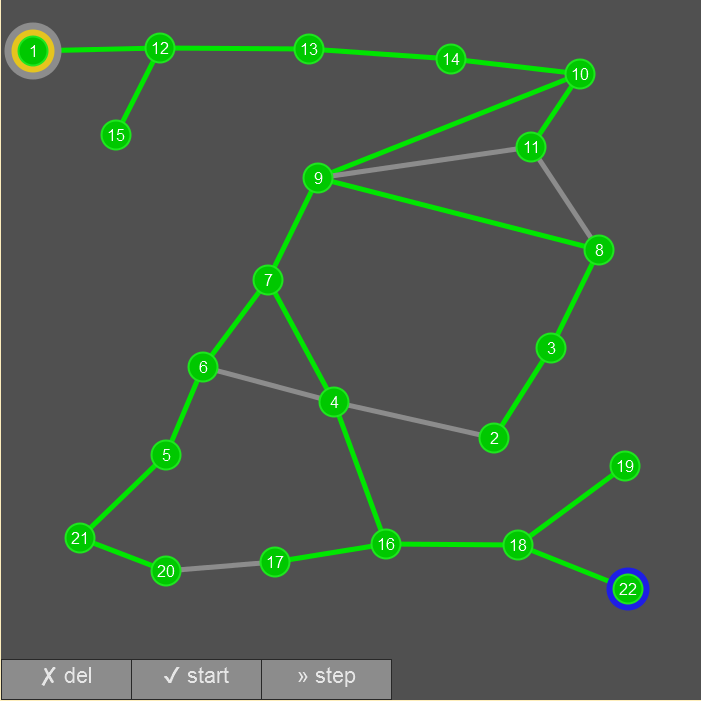
In einem Irrgarten wäre aber auch die Tiefensuche möglich. So hatte in der griechischen Mythologie Theseus den in einem Labyrinth versteckten Minotaurus zu töten. Die kluge Ariadne stattete Theseus mit einer Rolle Faden aus: Er band ein Fadenende am Eingang des Labyrinths fest und rollte den Faden beim Durchforschen des Labyrinths ab. So konnte er vermeiden, gleiche Teile des Labyrinths mehrfach zu durchsuchen, und fand zum Schluss auch wieder den Weg zurück zu Ariadne. Es gab ein Happyend, da er Minotaurus besiegte.
Der Faden wird als Ariadnefaden bezeichnet.
Welches ist der kürzeste Weg von A nach B? Diese Frage effizient zu beantworten ist nicht einfach. Mit der Simulation kann ein Wegnetz gezeichnet und nach der Festlegung von Start ⬤ und Ziel ⬤ die Suche schrittweise simuliert werden:
- Linksklick: neuer Ort (Knoten)
- Linksdrag und drop auf anderen Knoten: neue Strecke (Kante)
- je ein Linksklick auf bestehende Knoten: Zielort ⬤ → Startort ⬤ → normaler Knoten ⬤ festlegen
- Rechtsklick auf bestehenden Knoten: alle Kanten des Knotens entfernen
- 's': Start der Simulation
- 'n': neues Streckennetz anlegen
Beobachtungsaufgabe:
Versuchen Sie mit folgenden Simulationen herauszufinden, wie das Verfahren funktioniert:
- Simulation: lineares Strassennetz, d.h. eine einzelne Strecke mit mehreren Etappenorten.
- Simulation: mit einem Ort startend, verzweigt das Netz bei jedem Ort in zwei Strecken (binärer Baum).
- Simulation: komplexes Streckennetz mit beliebigem Start- und Zielort.
Hinweis: die Streckendistanz entspricht nicht genau der geometrischen Distanz, sondern variiert leicht zufällig. Dies imitiert eine nicht ganz lineare Streckenführung.
Lösungshinweise
Das Verfahren geht auf Edsger Wybe Dijkstra zurück, ein niederländischer Informatiker.
Vereinfacht lässt sich der Dijkstra-Algorithmus wie folgt beschreiben:
- markieren Sie den Startknoten gelb ⬤ und setzen Sie die Distanzzahl auf 0.
- für alle direkt benachbarten Knoten unternehmen Sie Folgendes:
- weist der Knoten noch keine Distanz auf (∞), so wird die Distanz zur Summe der Distanz des Startknotens plus jene zum Nachbarknoten.
- falls die Distanz des Knotens grösser ist als die Summe der Distanz des Startknotens plus jene zum Nachbarknoten, so notieren Sie diese Summe.
- markieren Sie den aktuellen Knoten mit gelb als besucht.
- markieren Sie den Startknoten grün ⬤ und die hinführende Strecke ebenfalls.
- Wählen Sie aus den gelb markierten Knoten jenen mit dem kleinsten Distanzwert aus. Sind mehrere Minimums vorhanden, wählen Sie einen beliebigen dieser Knoten.
- sind noch nicht alle Knoten markiert, so fahren Sie mit Punkt 2 weiter.