Galtonbrett Simulation
Denkanstoss 1
Wie gross ist die Wahrscheinlichkeit, dass bei einem Dreieck die Kugel links hinunterfällt?
Hinweis 1
Die Wahrscheinlichkeit, dass die Kugel links hinunterfällt, ist genau gleich gross wie diejenige, dass sie rechts hinunterfällt. Die Wahrscheinlichkeit ist also 1/2 oder 50%. Anders ausgedrückt ist die Wahrscheinlichkeit p, dass die Kugel links hinunterfällt, gleich 0.5.
Denkanstoss 2
Reduzieren Sie mit dem grünen Button die Levels auf 3. Wie gross ist die Wahrscheinlichkeit, dass eine Kugel auf allen drei Ebenen rechts vom Dreieck hinunterfällt, also ganz rechts zu liegen kommt?
Hinweis 2
Damit die Kugel ganz rechts zu liegen kommt, muss diese dreimal mit einer Wahrscheinlichkeit von 1/2 rechts hinunterfallen. Total also 1/2 * 1/2 * 1/2 = (1/2)3 = 1/8 = 0.125 = 12.5%.
Denkanstoss 3
Wie sieht die Wahrscheinlichkeit bei 4 Ebenen für das Fach ganz links aus?
Hinweis 3
Die Kugel muss viermal links hinunterfallen: (1/2)4 = 1/16 = 0.0625 = 6.25%.
Denkanstoss 4
Berechnen Sie für 4 Ebenen die Wahrscheinlichkeiten für alle fünf möglichen Fälle? Tipp: Errechnen Sie die Wahrscheinlichkeiten von oben nach unten.
Hinweis 4
Die Gesamtwahrscheinlichkeiten sehen wie folgt aus:
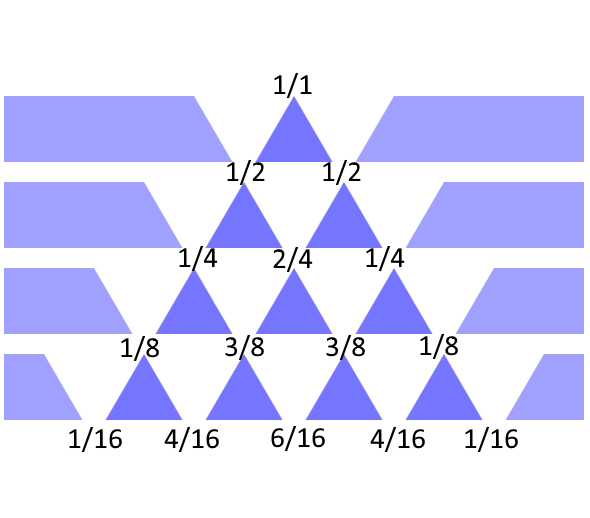
Zur direkten Berechnung der Wahrscheinlichkeiten machen Sie sich mit der Binomialverteilung und den Binomialkoeffizienten vertraut (z.B. bei Wikipedia Binomialverteilung und Wikipedia Binomialkoeffizient).
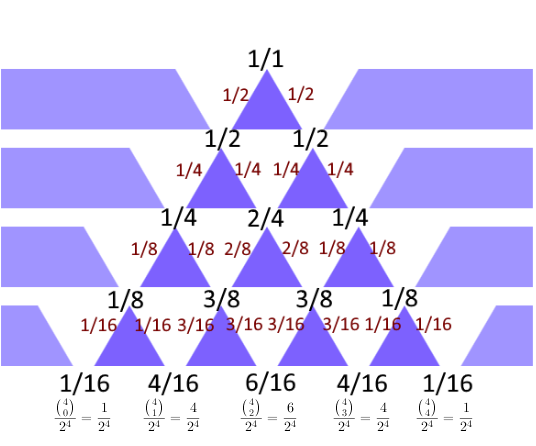
Denkanstoss 5
Erschliessen Sie sich den Zusammenhang zum Pascalschen Dreieck: Zahlenteufel.