Münzwurf-Simulation
Denkanstoss 1
Wie gross ist die Wahrscheinlichkeit, dass zwei von zwei geworfenen Münzen die Zahlseite zeigen?
Hinweis 1
Die Wahrscheinlichkeit, dass eine Münze mit der Zahl gegen oben zu liegen kommt ist 1/2 oder 50%. Anders ausgedrückt ist die Wahrscheinlichkeit p, dass eine Münze Zahl zeigt, gleich 0.5. Müssen beide geworfenen Münzen Zahl zeigen, so ist die kombinierte Wahrscheinlichkeit 0.5 * 0.5 = 0.25. D.h. im Durchschnitt wird jeder vierte Wurf zwei Zahlen zeigen. Stimmt das wirklich? Testen Sie dies mit der Simulation aus.
Denkanstoss 2
Wurf von zwei Münzen:
- Wie gross ist die Wahrscheinlichkeit, dass zweimal die Kopfseite erscheint?
- Wie gross ist die Wahrscheinlichkeit, dass einmal Kopf und einmal Zahl oben liegt?
Hinweis 2
Die Wahrscheinlichkeit, dass beide Münzen mit Kopf gegen oben zu liegen kommen, ist gleich der Wahrscheinlichkeit, dass zwei Zahlen nach oben schauen: p = 0.5 * 0.5 = 0.25.
Einmal Zahl und einmal Kopf kann auf zwei Arten zu Stande kommen:
- Die erste Münze zeigt Zahl und die zweite Münze zeigt Kopf.
- Die erste Münze zeigt Kopf und die zweite Münze zeigt Zahl.
Beide dieser Varianten haben eine Wahrscheinlichkeit von 0.5 * 0.5 = 0.25. Zusammen treten diese Varianten also mit p von 0.25 + 0.25 = 0.5 auf. Überprüfen Sie diese theoretischen Erwartungen mit der Simulation.
Denkanstoss 3
Wie verteilen sich die Wurfmuster, wenn eine grössere Anzahl Münzen sehr oft geworfen wird (z.B. 13 Münzen 1'000 mal)?
Hinweis 3
Die Balken verteilen sich symmetrisch zur Mittelachse in einer Art Glockenform.
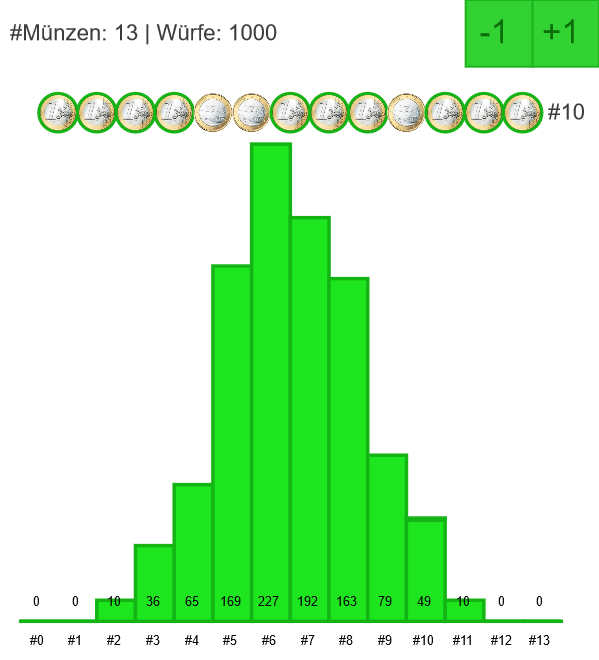
Denkanstoss 4
Berechnen Sie für das Verteilungsmuster aus Denkanstoss 3 die effektiv beobachteten relativen Häufigkeiten.
Wie gross muss die Summe aller errechneten relativen Häufigkeiten sein? Machen Sie den Kontrolltest.
Hinweis 4
Die beobachtete relative Häufigkeit errechnet sich aus der Anzahl Beobachtungen eines Musters dividiert durch die Gesamtzahl an Würfen. Z.B. bei 5 Zahlen (#5): p = 169 / 1000 = 0.169.
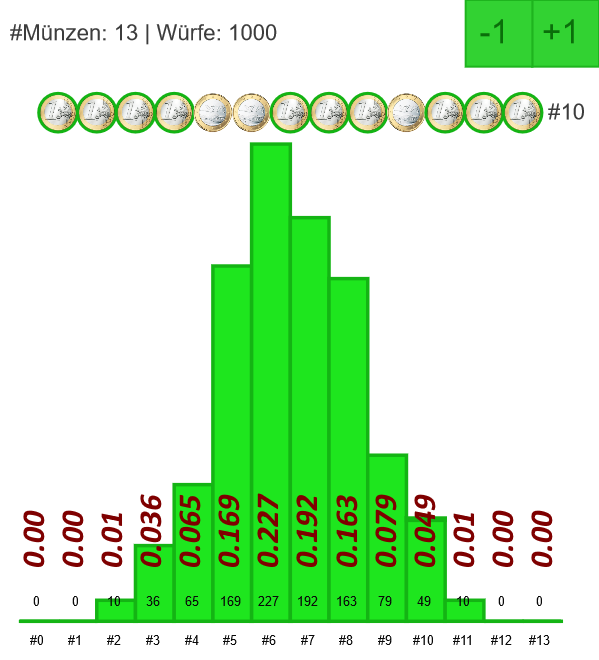
Die Summe über alle relativen Häufigkeiten muss genau 1 ergeben.
Denkanstoss 5
Wie lässt sich die theoretisch zu erwartende Wahrscheinlichkeit errechnen? Tipp: Machen Sie sich mit der Binomialverteilung und den Binomialkoeffizienten vertraut (z.B. bei Wikipedia Binomialverteilung und Wikipedia Binomialkoeffizient).
Hinweis 5
Die erwartete Wahrscheinlichkeit errechnet sich aus dem Binomialkoeffizienten dividiert durch 2 hoch Anzahl Münzen. Am Beispiel mit 13 Münzen und 5 Zahlen: 1287 / 213 = 1287 / 8192 = 0.157.
Online-Tool zur Berechnung der Binomialkoeffizienten oder auch manuell dank des Pascalschen Dreiecks (Zahlenteufel).

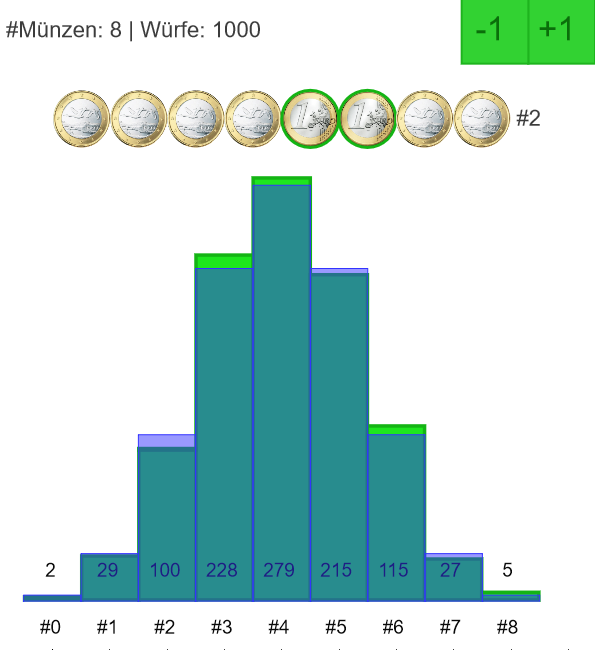
Bei der folgenden Simulation mit 1000 Würfen bei 8 Münzen ist die zu erwartende Verteilung als Binomialverteilung blau eingezeichnet. Die Abweichungen sind gut erkennbar.