Die Modulo-Operation ist Kern der diskreten Exponentialfunktion bx mod m. Bis heute ist für die Berechnung des Exponenten, wenn b und m gegeben ist, kein schneller Algorithmus bekannt. Daher wird die diskrete Exponentialfunktion als Einwegfunktion bei asymmetrischen Kryptosystemen eingesetzt. So z.B. beim Diffie-Hellman-Schlüsselaustausch.

Hinweise

• Verändern Sie mit den Pfeiltasten links | rechts den Exponenten x.
• Die Pfeiltasten oben | unten verändern den Divisor m.
• Beobachten Sie, wie bei unterschiedlichen Divisoren die Restwerte variieren.

Zusatzinfos

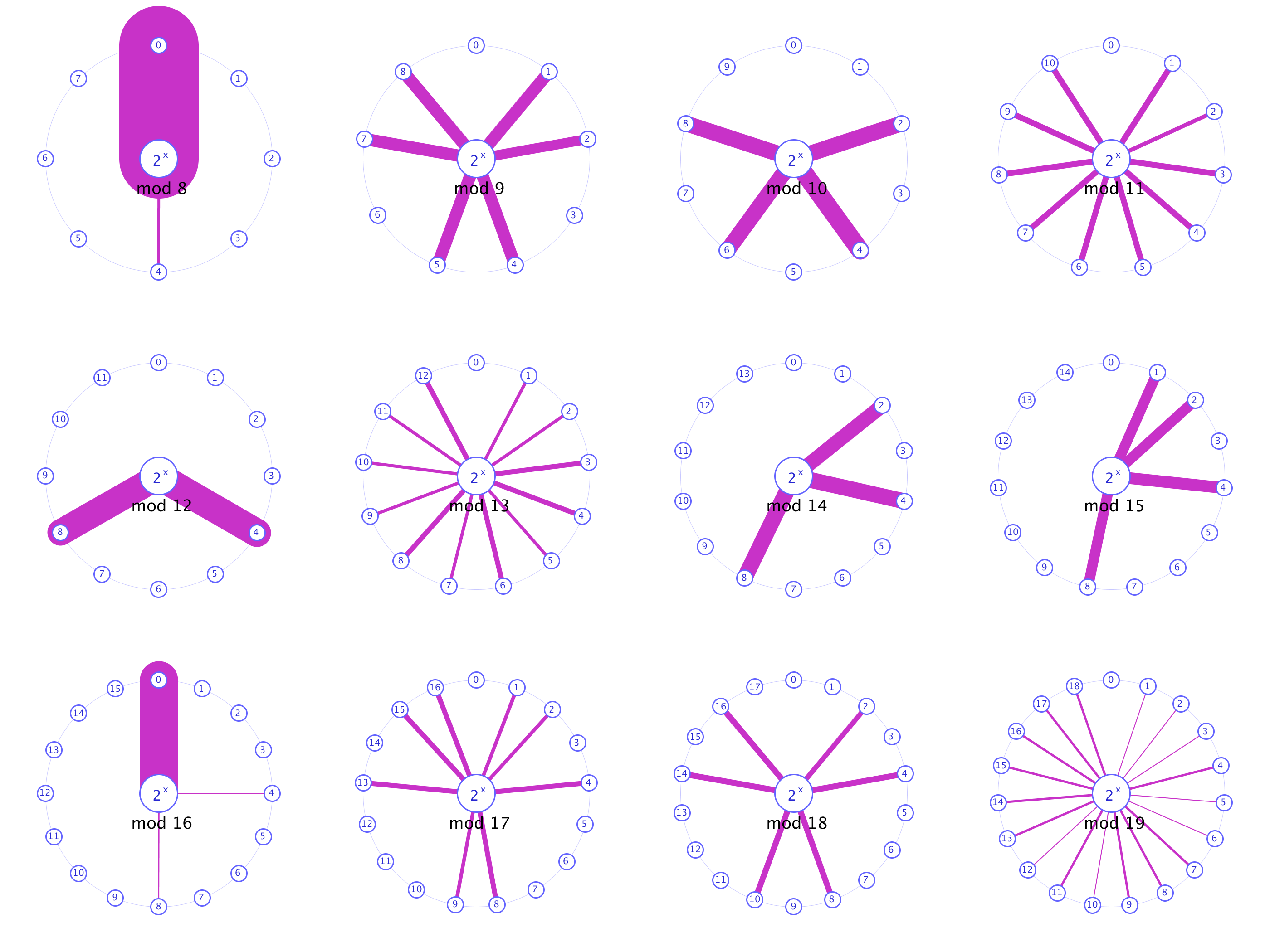
Je besser die Restwerte streuen, desto schwieriger wird der Angriff auf die Verschlüsselung auf Basis des entsprechenden Divisors. Besonders gut streuen die Restwerte bei Primzahlen wie z.B. 11, 13, 19, 29 oder 37.

Wie die Restwerte im Bereich 2¹ bis Bereich 2³¹ für die Divisoren 8 bis 19 variieren, zeigt folgende Darstellung. Die Dicke der Linien repräsentiert wie oft dieser Rest resultiert.