kleiner Gauss

Wie gross ist die Summe der ersten n aufeinanderfolgenden natürlichen Zahlen?

Man kann sich vorstellen, für i = 1 bis n jeweils i Farbpunkte auszulegen. Geschickt angeordnet bilden die Farbpunkte ein gleichschenkliges Dreieck.
Dies wird möglich, weil die Summen die arithmetische Reihe der Dreieckszahlen bilden.

Werden die Farbpunkte verdoppelt und in einem Rechteck angeordnet, so ist die ursprüngliche Anzahl Farbpunkte einfach zu berechnen: die Höhe multipliziert mit der Breite des Rechteckes dividiert durch zwei. Wird die Kantenlänge des Dreiecks mit n bezeichnet, lautet die Formel:

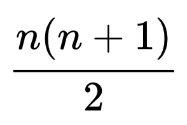
Diese Summenformel ist seit der vorgriechischen Mathematik bekannt, wurde aber gemäss Überlieferung vom Carl Friedrich Gauss als neunjähriger Schüler wiederentdeckt. Daher wird diese Summenformel auch kleiner Gauss genannt.