Einheitskreis: Grundlagen
Analysieren Sie den Zusammenhang zwischen dem Winkel im Einheitskreis und den Werten der Funktionen sin() und cos(). Einheitskreis meint einen Kreis mit Radius der Länge 1 und Mittelpunkt im Koordinatenursprung (0/0). Der Winkel im Zentrum wird meist mit φ bezeichnet.
Hinweis: bewegen Sie die Maus und betätigen Sie die Maustaste.
Koordinatensysteme: kartesische Koordinaten - Polarkoordinaten
Analysieren Sie den Zusammenhang zwischen kartesischem System links und dem Polarkoordinatensystem rechts. Der Winkel der Polarkoordinate wird meist mit φ bezeichnet.
Der Wertebereich von φ ist [0..2*π[.
Hinweise: Bewegen Sie den Punkt P mit den Pfeiltasten und verändern Sie die Anzeige mit der Maustaste. Zum Start muss die Simulation einmal angeklickt werden..
Einheitskreis: Winkelfunktionen sin() und cos()
Wie kommen die Werte der Winkelfunktionen sin() und cos() zu Stande?
Da der Einheitskreis einen Radius von 1 aufweist, ist die maximale horizontale und vertikale Auslenkung max. gleich 1. Die Auslenkung in x-Richtung abgetragen zeigt die cos()-Funktion im Wertebereich [0-360[ Grad beziehungsweise im Bereich [0..2π[ rad (Bogenmass). Die vertikale Auslenkung in y-Richtung lässt die Form der sin()-Funktion im gleichen Wertebereich entstehen.
Hinweis: bewegen Sie die Maus in der rechten Fensterhälfte und betätigen Sie die Maustaste.
Vektor
Bewegungen werden häufig mit einem Vektor abgebildet: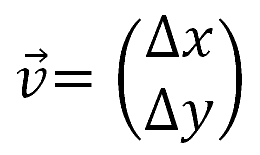 
. Die Simulation zeigt den Zusammenhang zu den Polarkoordinaten.