Cäsarcode
Beim Cäsarcode wird jedem Buchstaben des Klartexts ein Geheimtextbuchstabe zugeordnet, indem man das Alphabet um eine fixe Anzahl verschiebt (rotiert). Diese Anzahl nennt man Schlüssel. Er bleibt für die gesamte Verschlüsselung unverändert und dient mal -1 multipliziert zum Entschlüsseln des Geheimtextes. Es ist also ein symmetrisches Verfahren.
Klartext
Geheimtext
Dreh-Codierer
Ein kurzer Text kann in einem 6x6-Feld versteckt werden. Dazu wird eine Platzierungsvorlage in vier Richtungen auf das Feld gelegt und die Buchstaben vom Pfeil her oben links nach rechts unten eingefüllt. Mit den Tasten kann die Vorlage gedreht und ausgeblendet werden.
Hier findet sich eine Druckvorlage, um den Drehcodierer aus Papier zu basteln.
Vorlage drehen:
Klartext (max. 36 Zeichen)
Vigenère-Code
Beim Vigenère-Code wird jeder Buchstabe abhängig von seiner Position mit unterschiedlichem Abstand verschoben. Die Abstände werden mit einem Geheimwort bestimmt. Das Geheimwort wird wiederholt über den Klartext geschrieben. Je nach zugeordnetem Buchstabe wird unterschiedlich codiert. Papierversion
Schlüsselwort
Eingabetext
Ausgabetext
RSA-Zahlensets
Primzahlen und Primfaktoren finden
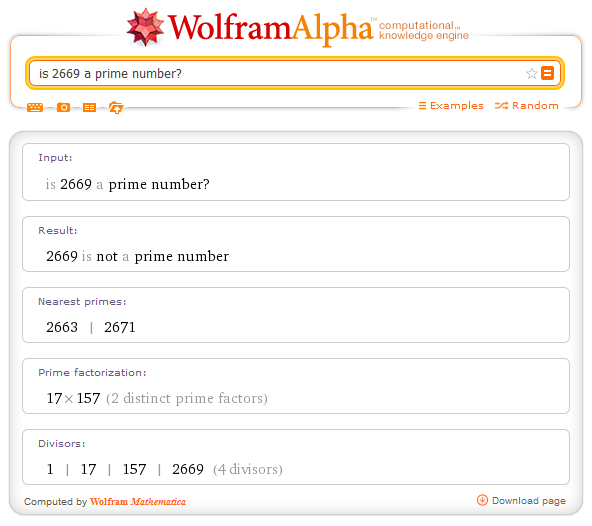
Als Unterstützung für das Finden von Primzahlen für p und q sowie von Faktoren zu m bietet sich Wolfram Alpha an. Die Antwort auf die Frage "is 2669 a prime number?" zeigt folgender Screenshot. In diesem Fall wird die Primzahl-Frage verneint und die vorhandenen Primfaktoren angezeigt. Die Primfaktoren zu einer Zahl lassen sich mit z.B. "factorization of 2669?" direkt anfordern. Dank Wolfram Alpha wird die Suche nach korrekten RSA-Zahlensets stark vereinfacht.