Download & erstes Programm
Unter Processing.org kann die Programmeirumgebung für Processing kostenlos für alle gängigen Betriebssysteme heruntergeladen werden. Die heruntergeladene ZIP-Datei muss entpackt werden. Anschliessend kann die Anwendung Processing gestartet werden.
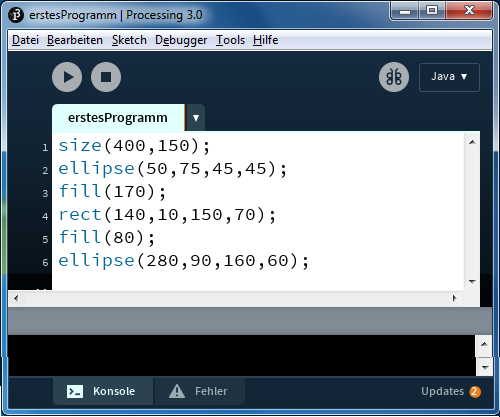
Der Editor ist sehr einfach aufgebaut und lässt sich intuitiv bedienen. Erste Anweisungen lassen sich mit Strichpunkten (;) getrennt eintippen und mit dem Run-Knopf austesten. Viel Erfolg!
✎ Aufgaben:
- Tippen Sie die Programmzeilen ab und lassen Sie das Programm laufen.
- Ändern Sie die Reihenfolge der Befehle. Was beobachten Sie?
- Verändern Sie die Parameter bei den Funktionen size(), ellipse(), rect() und fill(). Was bedeuten die einzelnen Parameter?
- Speichern Sie Ihren Sketch mit Namen "erstesProgramm".
Hinweis: Processing erstellt einen Ordner mit dem Programmnamen und darin die eigentliche Programmdatei mit gleichem Namen und der Erweiterung .pde. Diese beiden Namen müssen zwingend identisch sein. Belassen Sie die Ordner- oder Dateinamen unverändert.
Koordinatensystem
✎ Aufgaben:
- Studieren Sie mit der Simulation das Koordinatensystem von Processing.
- Welche Unterschiede zeigen sich zum kartesischen Koordinatensystem (vgl. Mathematik-Unterricht)?
Formen zeichnen
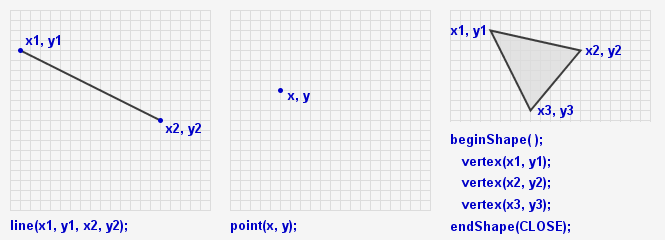
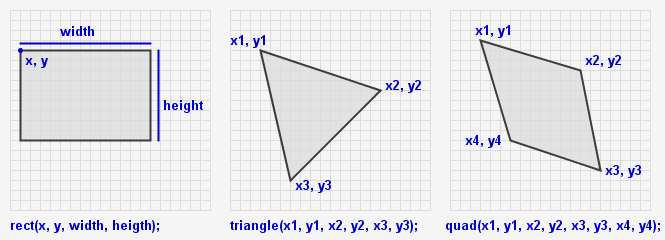
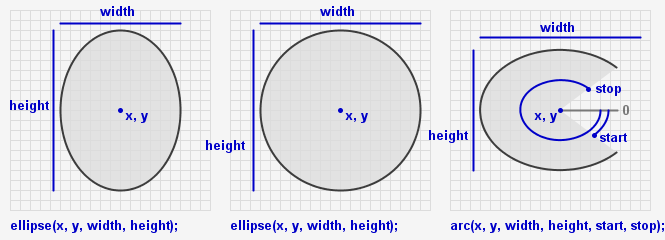
Alternativen:
- Kreis:
circle(x, y, d) - Quadrat:
square(x, y, s)
✎ Aufgaben:
- Erweitern Sie den Sketch "erstesProgramm" um mindestens 3 weitere Formen.
- Speichern Sie den neuen Sketch unter dem Namen "zweitesProgramm".
- Fakultativ: Studieren Sie die Zusatzinfos zu
arc().
Zusatzinfos arc()
Hinweis: Die Funktion radians() rechnet Grad (0 - 360) in Bogenmass (0 - 2*PI) um und die Funktion degrees() Bogenmass in Grad.
Hinweis: PI, TWO_PI, HALF_PI und QUARTER_PI sind Konstanten die in Processing zur Verfügung stehen.
Flächen färben
✎ Aufgaben:
- Testen Sie die vier Varianten der Funktion
fill( )mit Hilfe der Simulation. Was bedeuten jeweils die Parameter? - Übernehmen Sie den folgendnen Code in einen leeren Sketch und speichern Sie unter "meineFarben".
- Verändern Sie die Farb- und Deckkraft-Werte nach Ihrem Geschmack. Verwenden Sie dazu den ColorSelector von Processing unter Menu > Tools > ColorSelector. Speichern Sie den Sketch.
- Verändern Sie nun die Reihenfolge der Befehle in Ihrem Sketch. Was beobachten Sie? Speichern Sie unter "meineFarben2".
- Wenden Sie Ihr Wissen von der
fill( )-Funktion auf diebackground( )-Funktion an.
size(400,420); background(255); fill(51); ellipse(80,140,120,190); fill(152,204); ellipse(170,80,190,90); fill(229,152,0); ellipse(180,320,250,140); fill(39,229,52,205); ellipse(270,270,150,280);
Hinweis für Farbliebhaber: Neben dem hier gezeigten RGB-System kennt Processing auch das HSB-System. Konsultieren Sie dazu die Processing-Referenz.
Linien färben
✎ Aufgaben:
- Testen Sie die vier Varianten der Funktion
stroke( )mit Hilfe der Simulation. Was bedeuten jeweils die Parameter? - Übernehmen Sie den folgendnen Code in einen leeren Sketch und speichern Sie unter "meineFarben3". Variieren Sie die Farb-Parameter
- Fügen Sie die Funktionen
noStroke( )undnoFill( )ohne Parameter an verschiedenen Stellen im Code ein. Was bewirken diese?
size(400,420); background(255); strokeWeight(16); fill(160); stroke(50); ellipse(80, 140, 120, 190); stroke(153, 204); fill(83); ellipse(170, 80, 190, 90); stroke(229, 153, 0); fill(70, 121, 211); ellipse(180, 320, 250, 140); stroke(39, 229, 52, 205); fill(172, 85, 232); ellipse(270, 270, 150, 280);
grundlegende Datentypen
Variabeln dienen zur Speicherung von Daten. Daten werden auf dem Datenträger in binärer Form gespeichert, d.h. als Folgen aus lauter Einsen und Nullen. Acht Bit zusammen ergeben ein Byte, z.B. 01101011. Diese Zahlenfolge 011010112 entspricht 10710 im Dezimalsystem.
Simulation Binärsystem
Ein Bit kann man als Schalter mit den beiden Zuständen offen und zu. Nur wenn der Schalter geschlossen ist, fliesst Strom. Der offene Schalter wird mit 1 und der geschlossene Schalter mit 0 dargestellt.
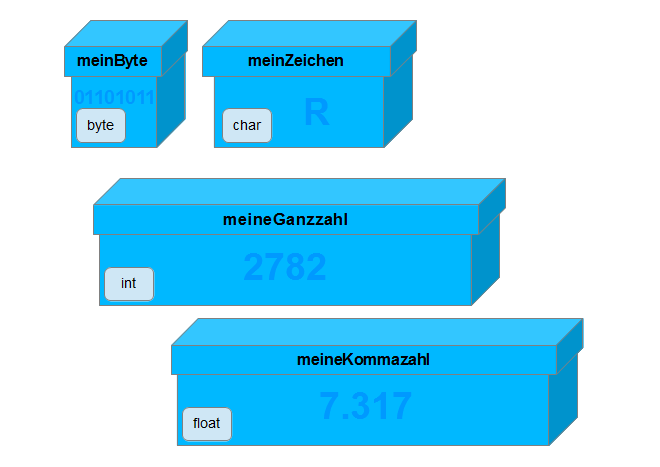
Variabeln kann man sich als Boxen vorstellen, die einen Datenwert aufnehmen können. Je nach Datentyp ist die Box unterschiedlich gross.
Folgende Standard-Datentypen kennt Processing:
| Datentyp | Speicherbedarf (Byte) | Wertebereich | Standardwert |
|---|---|---|---|
| byte | 1 | -128 bis +127 | 0 |
| short | 2 | -32768 bis +32767 | 0 |
| int | 4 | -2147483648 bis +2147483647 | 0 |
| long | 8 | -263 bis +263-1 | 0 |
| float | 4 | +- 3.40282347 * 1038 | 0.0 |
| double | 4 | +- 1.79769313 * 10308 | 0.0 |
| boolean | 1 | true, false | false |
| char | 2 | alle Unicodezeichen | |
| String | x*2 | Zeichenketten | |
Da je nach Datentyp unterschiedlich viel Speicherplatz benötigt wird, müssen Variablen deklariert werden. D.h. es muss der Datentyp und der Name der Variabeln festgelegt werden. Bei der Deklaration wird eine Box (vgl. Bild oben) der richtigen Grösse bereitgestellt und mit dem Variablennamen beschriftet.
// Deklaration byte meinByte; char meinZeichen; int meineGanzzahl; float meineKommazahl; String meineZeichenkette; //Initialisierung meinByte = 107; meinZeichen = 'R'; meineGanzzahl = 2782; meineKommazahl = 7.317; meineZeichenkette = "Hallo Welt";
Erst dank der Deklaration kann einer Variable ein Wert zugewiesen werden. Bei der ersten Wertzuweisung spricht man von der Initialisierung. Die Werte der Variablen können jederzeit ausgegeben oder für Berechnungen benutzt werden.
Wie der Name sagt, sind die Werte von Variabeln variabel. Die Werte können mit einer erneuten Wertzuweisung überschrieben, d.h. verändert, werden.
Deklaration und Initialisierung lassen sich in einer Anweisung kombinieren:
//Deklaration int a; int b; float v; // Deklaration + Initialisierung byte meinByte = 107; char meinZeichen = 'R'; int meineGanzzahl = 2782; float meineKommazahl = 7.317; String meineZeichenkette = "Hallo Welt"; // Wertzuweisungen a = meineGanzzahl; b = 31639 - meineGanzzahl; a = a * 2; v = meineKommazahl / 4; b = b + 100; meineZeichenkette = "Sprich: " + meineZeichenkette; // Ausgabe in Konsole println(a);
✎ Aufgaben:
- Übernehmen Sie den Code in einen leeren Sketch und speichern Sie unter Variablen2.
- Erweitern Sie die Konsolenausgabe so, dass auch die Variablen b, v und meineZeichenkette in der Konsole ausgeben werden.
- Ergänzen Sie die folgende Wertzuweisung
a = a * meineKommazahl. Was beobachten Sie? Wo liegt das Problem?
Hinweis: Die Funktion println() schreibt eine Zeile in die Konsole. print() generiert eine Konsolenausgabe ohne Zeilensprung. Mit diesen beiden Befehlen lassen sich verschiedenste Ausgaben realisieren:
println("Hallo mein Freund");
println("Wert der Variable a ist: " + a);
println(4*5/3.0);
print("meine Kommazahl beträgt: ");
print(meineKommazahl);
Tipp: Mit println()-Ausgaben lassen sich Fehler einfacher aufspüren, indem man an entscheidenden Stellen im Programmablauf den Wert von einer Variable ausgibt.
Operatoren
+ | Addition |
|---|---|
- | Subtraktion |
* | Multiplikation |
/ | Division |
= | Wertzuweisung |
Tipp: Die Zeichen für die Operationen finden sich am einfachsten im Zifferblock der Tastatur.
Hinweis: Wertzuweisungen werden wie folgt gelesen: x = x + 11 wird als "x wird zu x + 11" gelesen.
Globale & Lokale Variabeln
Wird eine Variable vor dem setup()-Block deklariert, so ist sie global sichtbar. D.h. man kann aus allen Codeblöcken heraus auf diese Variable zugreifen.
Wird dagegen eine Variable innerhalb eines Blocks, z.B. im draw()-Block deklariert, ist diese Variable nur innerhalb dieses Blocks sichtbar. Man spricht von einer lokalen Variablen.
Tipp: Verwenden Sie wo immer möglich lokale Variablen. So werden Fehler durch unbeabsichtigtes Überschreiben von Variabelnwerten minimiert.
Hinweis: Wird eine lokale Variable mit gleichem Namen wie eine globale Variable eingesetzt, so überdeckt die lokale Variable die globale. Im Notfall kann mit vorangestelltem this. auf die globale Variable zugegriffen werden. Z.B. a = this.meineZahl;.
//Deklaration globale Variabeln
int meineGanzzahl = 2782;
float meineKommazahl = 7.317;
void setup() {
// lokale Deklaration
int meineGanzzahl = 125;
float winkel = 2.0478;
println(meineGanzzahl);
println(meineKommazahl);
println(winkel);
println(this.meineGanzzahl);
}
void draw() {
// lokale Deklaration
int a = 353;
println(meineGanzzahl);
println(a);
println(winkel);
noLoop();
}
✎ Aufgaben:
- Studieren Sie den obigen Code. Was wird in der Konsole ausgegeben?
- Übernehmen Sie den Code in einen leeren Sketch und speichern Sie unter Variablen3. Testen Sie den Sketch und überprüfen Sie Ihre Antwort aus Frage 1.
- Verbessern Sie allfällige Fehler oder machen Sie fehlerhafte Zeilen zu Kommentaren, indem Sie
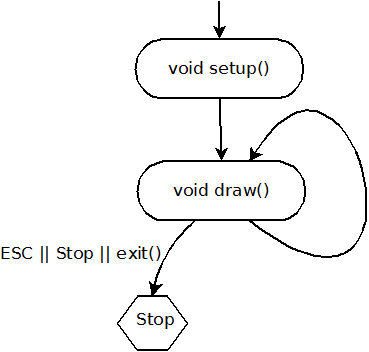
//voranstellen. - Was passiert, wenn Sie die Anweisung
noLoop()entfernen? Studieren Sie auch die folgende Abbidlung.

Datentyp color
Um Farben zu speichern, bietet Processing den Datentyp color an. Farben werden bekanntlich mit einem bis vier Parametern festgelegt. Die Funktion color() erstellt aufgrund der ihr übergebenen Parametern die eigentliche Farbe. So lassen sich Farben generieren und in Variablen speichern:
//Deklaration color meinGrau; color meinGrau2; color meineFarbe; color meineFarbe2; //Initialisierung meinGrau = color(100); // color(Grauwert) meinGrau2 = color(100,180); // color(Grauwert,Deckkraft) meineFarbe = color(255,190,40); // color(R,G,B) meineFarbe2 = color(255,190,40,180); // color(R,G,B,Deckkraft) fill(meinGrau); rect(0,0,60,60); fill(meinGrau2); rect(60,0,60,60); fill(meineFarbe); rect(120,0,60,60); fill(meineFarbe2); rect(180,0,60,60);
Der obige Code generiert folgendes Bild:

Datentyp Array
Eine Variable vom Typ Array, auch Datenfeld genannt, kann mehrere Werte des gleichen Typs speichern. Unter dem gleichen Namen lassen sich viele Werte abspeichern, die mit einem Index angesprochen werden. Die Nummerierung beginnt mit dem Index 0.
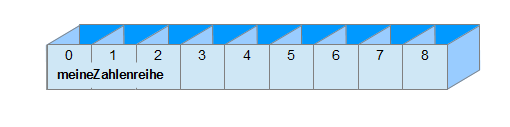
Hinweis: Beachten Sie, dass der letzte Index eines Arrays immer um 1 kleiner ist, als die Länge des Datenfeldes. Die Länge eines Arrays lässt sich mit der Funktion myArray.length ermitteln.
// Deklaration int[] meineZahlenreihe; // Initialisierung meineZahlenreihe = new int[9]; //Wertzuweisung meineZahlenreihe[0] = 4; meineZahlenreihe[3] = 132; meineZahlenreihe[5] = 71; // Konsolenausgabe println(meineZahlenreihe[3]); println(meineZahlenreihe[0]); println(meineZahlenreihe[8]); println(meineZahlenreihe); // gibt das ganze Array aus
✎ Aufgaben:
- Studieren Sie den obigen Code. Was wird in der Konsole ausgegeben?
- Was passiert wohl, wenn Sie
println(meineZahlenreihe[9]);einfügen? - Geben Sie die Länge des Arrays meineZahlenreihe in der Konsole aus.
- Geben Sie den Index des letzten Wertes des Arrays meineZahlenreihe in folgender Form in der Konsole aus:
der letzte Index von meineZahlenreihe ist: 8
Hinweis: Deklaration und Wertzuweisung lassen sich bei Arrays kombinieren:
// Deklaration
int[] meineZahlenreihe;
// Initialisierung & Zuweisung kombiniert
meineZahlenreihe = new int[] {5, -14, 67, 0, -2, 4};
2D-Array
Beim Programmieren sind zweidimensionale Arrays oft sehr hilfreich. So zum Abbilden eines Koordinatensystems wie in den Spielen "Vier gewinnt" oder "Schiffe versenken". Zweidimensionale Arrays lassen sich einfach deklarieren:
// Deklaration
int[][] meinKoordinatenfeld;
// Initialisierung & Zuweisung kombiniert
meinKoordinatenfeld = new int[][] {{1, 0, 2},{2, 2 , 0},{1, 0, 1}};
// Konsolenausgabe
println(meinKoordinatenfeld[1][2]);
// einzelne Wertzuweisung
meinKoordinatenfeld[1][2] = 1;
// Konsolenausgabe
println(meinKoordinatenfeld[1][2]);
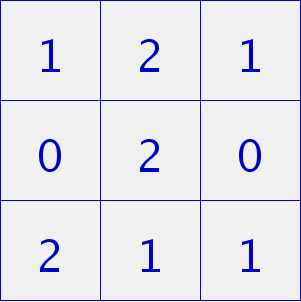
Die Ganzzahlen können als Code betrachtet werden:
- 0: leeres Spielfeld
- 1: Feld von Spieler 1 belegt
- 2: Feld von Spieler 2 belegt
Das erstellte Array sieht wie folgt aus:
Tipp: Für das Durchlaufen von 2D-Arrays sind verschachtelte for-Schleifen sinnvoll.
Systemvariabeln
| Name | Beschreibung |
|---|---|
mouseX | x-Koordinate der Maus |
mouseY | y-Koordinate der Maus |
pmouseX | vorherige x-Koordinate der Maus |
pmouseY | vorherige y-Koordinate der Maus |
mousePressed | ist TRUE wenn die Maustaste gedrückt, sonst FALSE |
width | Fensterbreite in Pixel |
height | Fensterhöhe in Pixel |
Systemkonstanten
PI | PI, 3.1415... |
|---|---|
TWO_PI | 2*PI |
HALF_PI | PI/2 |
QUARTER_PI | PI/4 |
Spezielle Datentypen in Processing
Systemfunktionen
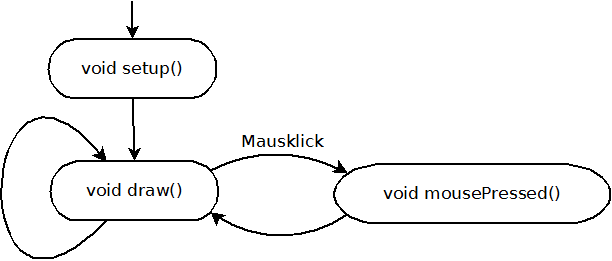
Funktionen sind Unterprogramme, die bestimmte, isolierte Aufgaben übernehmen. Bekannt sind die beiden Systemfunktionen void setup() und void draw().
Eine dritte zentrale Systemfunktion ist void mousePressed(). Sie wird bei Mausklick einmalig durchlaufen:
✎ Aufgabe:
Übernehmen Sie den folgenden Code in einen leeren Sketch und testen Sie die Funktionsweise von void mousePressed().
int rot = 45;
int gruen = 30;
int blau = 90;
void setup() {
size(200,100);
}
void draw() {
background(rot, gruen, blau);
}
void mousePressed() {
rot = rot + 30;
if (rot > 255) {
rot = 45;
}
}
Funktionen ohne Rückgabewert
Wir nehmen uns vor, einen Hund zu zeichnen. Damit es einfacher wird, verschieben wir mit translate(100,100) den Nullpunkt des Koordinatensystems zum Punkt 100/100. Dies ist zugleich die Mitte der Zeichnung. Nun können wir die verschiedenen Formen symmetrisch zur Mittelachse zeichnen. In der Skizze sind der Ursprung 0/0 und die Koordinaten der Mittelpunkte der Formen von Hand eingetragen.
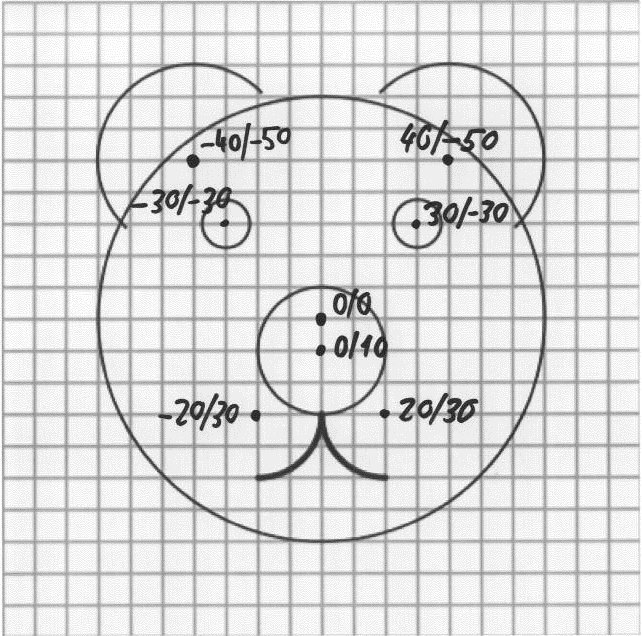
✎ Aufgabe:
Programmieren Sie einen Sketch, der einen Hund mit den skizzierten Dimensionen zeichnet.
Code Lösung
Der Code für den ganzen Hund sieht wie folgt aus:
void setup() {
size(200, 200);
smooth();
}
void draw() {
background(200);
translate(100, 100);
noFill();
strokeWeight(1);
stroke(90);
fill(30);
ellipse(-40, -50, 60, 60);
ellipse(40, -50, 60, 60);
fill(240);
ellipse(0, 0, 140, 140);
fill(30);
ellipse(-30, -30, 15, 15);
ellipse(30, -30, 15, 15);
ellipse(0, 10, 40, 40);
strokeWeight(2);
noFill();
arc(-20, 30, 40, 40, 0, HALF_PI);
arc(20, 30, 40, 40, HALF_PI, PI);
}
Um den Hund zu zeichnen sind viele Anweisungen notwendig und der void draw()-Block wird unübersichtlich. Es macht Sinn, den Code zum Zeichnen des Hundes in eine Funktion mit passendem Namen zu verpacken. Der Aufbau der selber gebauten Funktion ist gleich wie bei den System-Funktionen:
void meinHund() {
Anweisung 1;
...
Anweisung n;
}
Nun kann im void draw()-Block das Zeichnen des Hundes mit dem Aufruf der Funktion meinHund() übersichtlich ausgelöst werden.
Code
void setup() {
size(200, 200);
smooth();
}
void draw() {
background(200);
meinHund();
}
void meinHund() {
translate(100, 100);
noFill();
strokeWeight(1);
stroke(90);
fill(30);
ellipse(-40, -50, 60, 60);
ellipse(40, -50, 60, 60);
fill(240);
ellipse(0, 0, 140, 140);
fill(30);
ellipse(-30, -30, 15, 15);
ellipse(30, -30, 15, 15);
ellipse(0, 10, 40, 40);
strokeWeight(2);
noFill();
arc(-20, 30, 40, 40, 0, HALF_PI);
arc(20, 30, 40, 40, HALF_PI, PI);
}
PS: Das dem Funktionsnamen vorangestellte void zeigt an, dass die Funktion keinen Wert zurück liefert.
Funktionen mit Parametern

Nun möchten wir zwei Hunde zeichnen und zwar an verschiedenen Orten. Man könnte bei der ersten Version ohne Funktion einfach den Code verdoppeln, was aber zu einem extrem schlecht lesbaren Code führt.
Code-Verdoppelung
Kein vorbildlicher Code!
void setup() {
size(400, 200);
smooth();
}
void draw() {
background(230);
translate(100,100);
noFill();
strokeWeight(1);
stroke(90);
fill(30);
ellipse(-40, -50, 60, 60);
ellipse(40, -50, 60, 60);
fill(240);
ellipse(0, 0, 140, 140);
fill(30);
ellipse(-30, -30, 15, 15);
ellipse(30, -30, 15, 15);
ellipse(0, 10, 40, 40);
strokeWeight(2);
noFill();
arc(-20, 30, 40, 40, 0, HALF_PI);
arc(20, 30, 40, 40, HALF_PI, PI);
translate(200,0);
noFill();
strokeWeight(1);
stroke(90);
fill(30);
ellipse(-40, -50, 60, 60);
ellipse(40, -50, 60, 60);
fill(240);
ellipse(0, 0, 140, 140);
fill(30);
ellipse(-30, -30, 15, 15);
ellipse(30, -30, 15, 15);
ellipse(0, 10, 40, 40);
strokeWeight(2);
noFill();
arc(-20, 30, 40, 40, 0, HALF_PI);
arc(20, 30, 40, 40, HALF_PI, PI);
}
Bedeutend einfacher ist, der Funktion die Koordinaten für den Mittelpunkt des Hundes zu übergeben. Der Funktionskopf wird mit den beiden Parametern xPos und yPos ergänzt. Zu jedem Paramter muss der Datentyp deklariert werden, damit die Funktion entsprechende Variablen bereit stellen kann. In unserem Fall sind dies Ganzzahlen vom Datentyp int.
Im void draw()-Block wird nun die Funktion zweimal aufgerufen und zwar mit unterschiedlichen Koordinaten. Die übergebenen Paramter müssen genau den im Funktionskopf bestimmten Datentypen entsprechen. Hier werden zwei Parameter, beides Ganzzahlen, erwartet.
void setup() {
size(400, 200);
smooth();
}
void draw() {
background(200);
meinHund(100,100);
meinHund(300,100);
}
void meinHund(int xPos, int yPos) {
pushMatrix(); // bisheriger 0/0-Punkt wird zwischengespeichert
translate(xPos, yPos);
noFill();
strokeWeight(1);
stroke(90);
fill(30);
ellipse(-40, -50, 60, 60);
ellipse(40, -50, 60, 60);
fill(240);
ellipse(0, 0, 140, 140);
fill(30);
ellipse(-30, -30, 15, 15);
ellipse(30, -30, 15, 15);
ellipse(0, 10, 40, 40);
strokeWeight(2);
noFill();
arc(-20, 30, 40, 40, 0, HALF_PI);
arc(20, 30, 40, 40, HALF_PI, PI);
popMatrix(); // zuletzt zwischengespeicherter 0/0-Punkt wird wieder hergestellt
}
PS: Eine selber definierte Funktion mit Parametern funktioniert genau gleich wie von Processing zur Verfügung gestellte Funktionen, z.B. rect(x,y,width,height) oder random(0,26).

✎ Aufgabe:
Erweitern Sie die Parameter der Funktion meinHund() so, dass auch der Grauwert zur Füllung des Gesichts und die Grösse des Gesichts übergeben werden.
Tipp: Die Grösse kann am einfachsten mit der scale()-Anweisung gesteuert werden.
Lösung
void setup() {
size(400, 200);
smooth();
}
void draw() {
background(200);
meinHund(100,100,245,1.1);
meinHund(240,80,200,0.6);
meinHund(320,110,225,0.9);
}
void meinHund(int xPos, int yPos, int grau, float sFaktor) {
pushMatrix(); // bisheriger 0/0-Punkt wird zwischengespeichert
translate(xPos, yPos);
scale(sFaktor); // Zeichenfläche skalieren
noFill();
strokeWeight(1);
stroke(90);
fill(30);
ellipse(-40, -50, 60, 60);
ellipse(40, -50, 60, 60);
fill(grau);
ellipse(0, 0, 140, 140);
fill(30);
ellipse(-30, -30, 15, 15);
ellipse(30, -30, 15, 15);
ellipse(0, 10, 40, 40);
strokeWeight(2);
noFill();
arc(-20, 30, 40, 40, 0, HALF_PI);
arc(20, 30, 40, 40, HALF_PI, PI);
popMatrix(); // zuletzt zwischengespeicherter 0/0-Punkt wird wieder hergestellt
}
Funktionen mit Rückgabewert
Die bisher angeschauten Funktionen hatten den Rückgabetyp void. Sie liefern also keinen Wert zurück. Folgende Systemfunktionen liefern ebefalls keinen Wert zurück:
fill(r,g,b);noStroke();line(x1,y1,x2,y2);arc(x,y,w,h,start,end);- und viele mehr ...
Viele Funktionen liefern aber einen Wert zurück. Bekannte Systemfunktionen mit Rückgabewert sind:
sin(winkel);sq(zahl);sqrt(zahl);min(zahl1, zahl2 [, zahlX]);dist(x1,y1,x2,y2);- und viele andere ...
Aufgabe
Testen Sie den folgenden Sketch:
In diesem Sketch ist eine Funktion eingebaut, die die Fläche des Rechtecks berechnet und zurückliefert. Der Rückgabewert ist vom Typ int.
Der Code zeigt die Besonderheiten
- Aufruf der Funktion aus dem
void draw()-Block heraus - Beim Aufruf werden die zwei Parameter
mouseXundmouseYmitgegeben. - Im Funktionskopf ist dem Funktionsnamen
rechteckFlaecheder Rückgabetypintvorangestellt. - Die Funktion erwartet zwei Parameter vom Typ
intund übernimmt die Werte in die Variablenlaengeundbreite. - Die Funktion berechnet die Fläche und speichert diese in der Variablen
flaeche. - Zum Schluss liefert die Funktion den Wert der Variablen
flaechemitreturnzurück.
// Variable zur Speicherung des Rückgabewertes der Funktion
int groesse;
void setup() {
size(660, 120);
}
void draw() {
background(230);
fill(255,196,46);
rect(0, 0, mouseX, mouseY);
// Funktionsaufruf u. Zuweisung des Rückgabewertes an Variable
groesse = rechteckFlaeche(mouseX, mouseY);
// Textausgabe der Reckteckfläche
fill(30);
text("Fläche: " + groesse + " Pixel", 5, 15);
}
// eigene Funktion mit Rückgabewert vom Typ int
int rechteckFlaeche(int laenge, int breite) {
int flaeche = laenge * breite; // Fläche berechnen
return flaeche; // Resultat zurückgeben
}
✎ Aufgabe:
Studieren Sie den folgenden Sketch und programmieren Sie ihn nach. Setzen Sie eine Funktion zur Berechnung der Mondanziehung ein. Die Mondanziehung ist nur rund 0.165 mal so stark wie die Erdanziehung.
Lösung
float mErde; // Masse auf der Erde
float mMond; // Masse auf dem Mond
void setup() {
size(300, 300);
}
void draw() {
mErde = height-constrain(mouseY,20,height); // constrain = begrenzen
mMond = umrechnerErdeMond(mErde); // Funktionsaufruf
background(245);
// Säule Erde
fill(46, 46, 255);
text("Erde:",20,height-5);
rect(60, height, 60, -mErde);
// Säule Mond
fill(247, 132, 7);
text("Mond:",140,height-5);
rect(180, height, 60, -mMond);
fill(30);
// Beschriftung beider Werte
text(nf(mErde,1,1)+" kg",70,height-mErde-5);
text(nf(mMond,1,1)+" kg",190,height-mMond-5);
}
// eigene Funktion
// Rückgabewert-Typ Funktionsname (Datentyp Parameter)
float umrechnerErdeMond(float gewichtErde) {
float resultat;
resultat = gewichtErde * 0.165; // Berechnung
return resultat; // Rückgabe des Ergebnisses
}
Abschluss-Übung
Schreiben Sie analog zum Beispiel Hund einen Sketch, der folgenden Comic mit Hilfe einer Funktion und der Übergabe von Parametern zeichnet.
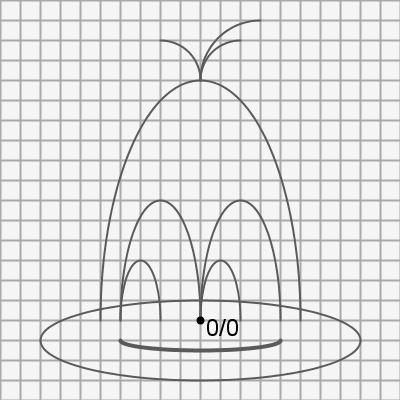

Hinweise:
- Der Ursprung 0/0 wird für das Zeichnen verschoben (vgl. Skizze).
- Es wird v.a. die Form
arc()verwendet. Beachten Sie dazu das Kapitel Einleitung > Formen zeichnen > Zusatzinfos zu arc(). - Gehen Sie etappiert vor. Z.B.:
- In der Skizze oben links Formen und ihre Koordinaten bestimmen.
- Comic zuerst im Hauptprogramm, genauer im
void draw()-Block, zeichnen. - Das Zeichnen in eine eigene Funktion auslagern.
- Funktion um Paramter ergänzen: z.B. Farbe und Grösse.
- Funktion mehrmals mit unterschiedlichen Parametern aus dem
void draw()-Block heraus aufrufen.
mögliche Ausgabe:

Lösung: Code für ein Gesicht
color meineFarbe = color(255,196,46); translate(100,160); strokeWeight(1); stroke(90); // Stirn fill(meineFarbe); arc(0,0,100,240,PI,TWO_PI); // Augen fill(230); arc(-20,0,40,120,PI,TWO_PI); arc(20,0,40,120,PI,TWO_PI); // Pupillen fill(30); arc(-30,0,20,60,PI,TWO_PI); arc(10,0,20,60,PI,TWO_PI); // Haare noFill(); arc(-20,-120,40,40,PI+HALF_PI,TWO_PI); arc(30,-120,60,60,PI,PI + HALF_PI); arc(20,-120,40,40,PI,PI + HALF_PI); // Mundpartie fill(meineFarbe); ellipse(0,10,160,40); // Mund stroke(30); strokeWeight(2); noFill(); arc(0,10,80,10,0,PI);
Lösung: Code für eine Serie Gesichter
color myColor;
void setup() {
size(660, 240);
smooth();
}
void draw() {
background(245);
myColor = color(255,196,46);
comicZeichnen(100,160,myColor,1);
myColor = color(204,189,16);
comicZeichnen(220,120,myColor,0.8);
myColor = color(127,98,23);
comicZeichnen(430,150,myColor,0.7);
myColor = color(16,165,201);
comicZeichnen(350,190,myColor,1.2);
myColor = color(162,47,245);
comicZeichnen(550,170,myColor,1.1);
}
void comicZeichnen(int xPos, int yPos, color meineFarbe, float sFaktor) {
pushMatrix(); // bisheriger 0/0-Punkt wird zwischengespeichert
translate(xPos, yPos);
scale(sFaktor); // Zeichenfläche skalieren
strokeWeight(1);
stroke(90);
// Stirn
fill(meineFarbe);
arc(0,0,100,240,PI,TWO_PI);
// Augen
fill(230);
arc(-20,0,40,120,PI,TWO_PI);
arc(20,0,40,120,PI,TWO_PI);
// Pupillen
fill(30);
arc(-30,0,20,60,PI,TWO_PI);
arc(10,0,20,60,PI,TWO_PI);
// Haare
noFill();
arc(-20,-120,40,40,PI+HALF_PI,TWO_PI);
arc(30,-120,60,60,PI,PI + HALF_PI);
arc(20,-120,40,40,PI,PI + HALF_PI);
// Mundpartie
fill(meineFarbe);
ellipse(0,10,160,40);
// Mund
stroke(30);
strokeWeight(2);
noFill();
arc(0,10,80,10,0,PI);
popMatrix(); // zuletzt zwischengespeicherter 0/0-Punkt wird wieder hergestellt
}
Zusatzaufgabe für Profis
Erweitern Sie die Comicgesichter derart, dass die Pupillen dem Mauszeiger folgen. Beispiel:
Interaktionen
mousePressed
✎ Aufgaben:
- Öffnen Sie in Processing einen neuen Sketch
- Übernehmen Sie den Programmcode indem Sie auf den Link "View Raw Code" rechts oben klicken, den Code markieren, kopieren und in Processing einfügen. ➤ Run!
- Testen Sie die Funktion der Maustaste.
- Verändern Sie die Farben mit Ihrem Vorwissen.
- Verändern Sie die gezeichnete Form z.B. zu einem Pacman.
- Speichern Sie den Sketch unter "interact1".
void setup() {
size(480, 280);
smooth();
}
void draw() {
if (mousePressed == true) {
fill(70);
}
else {
fill(180);
}
ellipse(mouseX, mouseY, 60, 60);
}
In der Systemvariable mouseButton wird entweder LEFT, RIGHT oder CENTER gespeichert. Mit if (mouseButton == LEFT) {...} kann zum Beispiel ein Linksklick gestgestellt werden.
✎ Erweiterung:
Ergänzen Sie den obigen Code so, dass sich die Farbe der Kreise in Abhängigkeit von der gedrückten Maustaste ändert.
Lösung Erweiterung
void setup() {
size(480, 280);
smooth();
}
void draw() {
if (mousePressed) {
if (mouseButton == LEFT) {
fill(210, 50, 50);
}
if (mouseButton == CENTER) {
fill(50, 210, 50);
}
if (mouseButton == RIGHT) {
fill(50, 50, 210);
}
}
else {
fill(180);
}
ellipse(mouseX, mouseY, 60, 60);
}
void mousePressed()
Mouse-Events können auch in separaten Systemfunktionen abgearbeitet werden. Zur Verfügung stehen:
mousePressed() | Code wird bei Mausklick einmal ausgeführt |
|---|---|
mouseReleased() | Code wird beim Loslassen eines Mausbuttons einmal ausgeführt |
mouseMoved() | Code wird beim Bewegen der Maus einmal ausgeführt |
mouseDragged() | Code wird beim Bewegen der Maus bei gehaltener Maustaste einmal ausgeführt |
Beispiel
// globale Variabeln
int xMuenze;
int yMuenze;
int dMuenze= 30; // Durchmesser der Muenze
int xZiel;
int yZiel;
int dZiel = 70; // Durchmesser des Ziels
// setup() wird beim Start einmal ausgeführt
void setup() {
size(250,250);
xMuenze = 40;
yMuenze = 35;
xZiel = width/2;
yZiel = height/2;
}
// draw() wird wiederholt
void draw() {
background(230);
fill(50);
ellipse(xZiel, yZiel, dZiel, dZiel);
fill(210, 50, 50);
ellipse(xMuenze, yMuenze, dMuenze, dMuenze);
}
// wird ausgeführt, wenn die Maus gedrückt bewegt wird
void mouseDragged() {
xMuenze = mouseX;
yMuenze = mouseY;
}
✎ Aufgaben:
- Übernehmen Sie den Code und speichern Sie den Sketch unter "interact2". Studieren und experimentieren Sie mit dem Code.
- Erweitern Sie den Code derart, dass sobald die rote Muenze über dem Schwarzen Loch (=Ziel) ist, der Hintergrund grün wird. Speichern Sie unter "interact2b".
Tipp: verwenden Sie die Funktiondist()im Blockdraw(). - Ergänzen Sie nun eine Mausevent-Routine, die beim Loslassen der Maus prüft, ob die Muenze über dem Schwarzen Loch liegt. Falls ja, soll die Muenze auf die Startposition zurück gesetzt werden. Speichern Sie unter "interact2c".
Tipp: Fügen Sie eine zumouseDragged()analoge Prozedur ein.
Testen Sie das fertige Programm:
Lösung Aufgabe 2
// globale Variabeln
int xStart = 40;
int yStart= 35;
int xMuenze;
int yMuenze;
int dMuenze= 30; // Durchmesser der Muenze
int xZiel;
int yZiel;
int dZiel = 70; // Durchmesser des Ziels
float abstand; // Abstand zum Ziel
// setup() wird beim Start einmal ausgeführt
void setup() {
size(250, 250);
xMuenze = xStart;
yMuenze = yStart;
xZiel = width/2;
yZiel = height/2;
}
// draw() wird wiederholt
void draw() {
abstand = dist(xMuenze, yMuenze, xZiel, yZiel);
if (abstand < dZiel/2 - dMuenze/2) {
background(50, 230, 50);
}
else {
background(230);
}
fill(50);
ellipse(xZiel, yZiel, dZiel, dZiel);
fill(210, 50, 50);
ellipse(xMuenze, yMuenze, dMuenze, dMuenze);
}
// wird ausgeführt, wenn die Maus gedrückt bewegt wird
void mouseDragged() {
xMuenze = mouseX;
yMuenze = mouseY;
}
// wird einmal ausgeführt, wenn die Maustaste losgelassen wird
void mouseReleased() {
xMuenze = xStart;
yMuenze = yStart;
}
Anregung
Erweitern Sie den obigen Sketch zu einem einfachen Spiel:
- Positionieren Sie die Münze beim Zurücksetzen zufällig: random().
- Zählen Sie je einen Punkt beim korrekten Versenken der Münze.
- Messen Sie die verstreichende Zeit.
- Geben Sie die durchschnittlichen Punkte pro Sekunde aus. Tipp: verwenden Sie
frameCountundframeRatean Stelle von Zeitfunktionen wieminute(), second()etc. - ...
Viel Spass!
keyPressed
Die Systemvariable keyPressed funktioniert analog zu mousePressed
void setup() {
size(480, 280);
smooth();
}
void draw() {
if (keyPressed == true) {
fill(70);
}
else {
fill(180);
}
ellipse(mouseX, mouseY, 60, 60);
}
In der Systemvariable key wird der gedrückte Buchstabe gespeichert. Mit if (key == 's' || key == 'S') {...} kann zum Beispiel auf die Eingabe von 's' oder 'S' getestet werden.
✎ Erweiterung:
Ergänzen Sie den obigen Code so, dass die Farbe nur ändert wenn 'f' oder 'F' gedrückt wird.
Lösung Erweiterung
void setup() {
size(480, 280);
smooth();
}
void draw() {
if (keyPressed == true && key == 'f' || key == 'F') {
fill(70);
}
else {
fill(180);
}
ellipse(mouseX, mouseY, 60, 60);
}
keyPressed()
Key-Events können in der Systemfunktionen keyPressed() abgearbeitet werden. Zur Verfügung stehen folgende Variabeln oder Funktionen:
keyPressed() | Systemfunktion wird beim Drücken einer Taste einmal ausgeführt. Die gedrückte Taste wird in der Systemvariable key gespeichert. |
|---|---|
keyReleased() | Systemfunktion wird beim Loslassen einer Taste einmal ausgeführt. Die losgelassene Taste wird in der Systemvariable key gespeichert. |
key | Systemvariable für das Erkennen welche Taste gedrückt wurde. Beispiel: if (key == 'b' || key == 'B') {...} |
keyCode | Systemvariable für das Erkennen von Spezialtasten wie die Pfeiltasten UP, DOWN, LEFT, RIGHT und ALT, CONTROL, SHIFT. Beispiel: if (keyCode == UP) {...}Achtung, die Spezialtasten BACKSPACE, TAB, ENTER, RETURN, ESC und DELETE werden nicht codiert und müssen direkt mit key verarbeitet werden. Beispiel: if (key == BACKSPACE) {...} |
✎ Vorbereitung:
Anhand eines kleinen Spiels sollen die Möglichkeiten der Key-Events gezeigt werden. Zuerst wird ein einfaches Raumschiff entworfen. Wie kann dieses Raumschiff möglichst einfach gezeichnet werden?
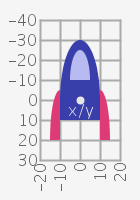
Lösung Vorbereitung
Das Raumschiff ist mit Kreisbogen, arc(x, y, breite, höhe, startWinkel, endWinkel), einfach zu zeichnen. Mit einem Rechteck ergänzt ist der Raumgleiter schon fertig. In der folgenden Skizze sind nur die Umrisse und Ursprünge der Formen eingezeichnet.
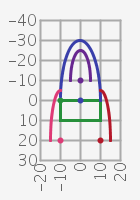
fill(57,63,170); noStroke(); arc(0, 0, 20, 60, PI, TWO_PI); rect(-10,0,20,10); fill(183,187,242); arc(0, -10, 10, 30, PI, TWO_PI); fill(222,58,118); arc(-10, 20, 10, 50, PI, PI + HALF_PI); arc(10, 20, 10, 50, PI + HALF_PI, TWO_PI);
Tipp: mit translate(x,y) kann vor dem Zeichnen der Ursprung an die gewünschte Position verschoben werden und anschliessend mit translate(-x,-y) wieder zurück.
✎ Einstiegsaufgaben:
- Öffnen Sie in Processing einen neuen Sketch.
- Übernehmen Sie den untenstehenden Programmcode mit "View Raw Code" rechts oben, Code markieren, kopieren und in Processing einfügen. ➤ Run!
- Testen Sie die Funktion der Pfeiltasten.
- Studieren Sie den Code: Welche Funktionen kommen zum Einsatz?
- Ergänzen Sie den Code, so dass das Raumschiff nach rechts gesteuert werden kann.
- Speichern Sie den Sketch unter "interact4b".
int schritt = 3;
int xRaumschiff; // x-Position des Raumschiffs
void setup() {
size(280, 140);
smooth();
xRaumschiff = width/2; // x-Startposition festlegen
}
void draw() {
background(150);
raumschiffZeichnen(xRaumschiff,height-25);
}
void raumschiffZeichnen(int xPos, int yPos) {
translate(xPos, yPos); // Zeichnenursprung verschieben
fill(57,63,170);
noStroke();
arc(0, 0, 20, 60, PI, TWO_PI);
rect(-10,0,20,10);
fill(183,187,242);
arc(0, -10, 10, 30, PI, TWO_PI);
fill(222,58,118);
arc(-10, 20, 10, 50, PI, PI + HALF_PI);
arc(10, 20, 10, 50, PI+ HALF_PI, TWO_PI);
translate(-xPos, yPos); // Zeichnenursprung zurück verschieben
}
void keyPressed() {
if (keyCode == LEFT) {
xRaumschiff = xRaumschiff - schritt;
if (xRaumschiff < 0) {
xRaumschiff = width;
}
}
}
✎ Erweiterung 1:
Ergänzen Sie den obigen Code so, dass das Raumschiff erst mit 's' oder 'S' gestartet wird. Der Sketch soll sich wie hier verhalten:
Tipp: Für Schalter wie "gestartet" oder "nicht gestartet" eignet sich der Datentyp boolean.
Lösung Erweiterung 1
int schritt = 3;
int xRaumschiff;
boolean gestartet = false;
void setup() {
size(280, 140);
smooth();
xRaumschiff = width/2;
}
void draw() {
background(150);
if (gestartet == false) {
fill(255);
text("'s' für Start", 10, 20);
text("bewegen mit den Pfeiltasten links | rechts", 10, 40);
}
raumschiffZeichnen(xRaumschiff, height-25);
}
void raumschiffZeichnen(int xPos, int yPos) {
translate(xPos, yPos);
fill(57, 63, 170);
noStroke();
arc(0, 0, 20, 60, PI, TWO_PI);
rect(-10, 0, 20, 10);
fill(183, 187, 242);
arc(0, -10, 10, 30, PI, TWO_PI);
fill(222, 58, 118);
arc(-10, 20, 10, 50, PI, PI+ HALF_PI);
arc(10, 20, 10, 50, PI+ HALF_PI, TWO_PI);
translate(-xPos, yPos);
}
void keyPressed() {
if (key == 's' || key == 'S') {
gestartet = true;
}
if (gestartet == true) {
if (keyCode == LEFT) {
xRaumschiff = xRaumschiff - schritt;
if (xRaumschiff < 0) {
xRaumschiff = width;
}
}
if (keyCode == RIGHT) {
xRaumschiff = xRaumschiff + schritt;
if (xRaumschiff > width) {
xRaumschiff = 0;
}
}
}
}
✎ Erweiterung 2:
Nun soll das Raumschiff durch das Weltall fliegen und Planeten und Gaswolken begegnen:
- Platzieren Sie die beiden folgenden Grafiken mit Hilfe von
image(bild, xPos, yPos)im Sketch.
Tipp: verwenden Sie den DatentypPImageund die BildausrichtungimageMode(CENTER). - Fügen Sie ein Variable
vfür die Geschwindigkeit der Objekte ein. Bewegen Sie die Objekte bei jedem Durchlauf vondraw()in y-Richtung um den Wert vonv. - Setzen Sie die Objekte nach Verlassen des Bildschirms zurück an den oberen Rand.
- Variieren Sie beim Zurücksetzen der Objekte an den oberen Rand ihre x-Position mit Hilfe einer Zufallszahl:
random(0,width).
So könnte die Lösung funktionieren - bitte antesten:
Lösung Erweiterung 2
int schritt = 4;
int xRaumschiff;
boolean gestartet = false;
// Variablen für die beiden Bilder deklarieren
PImage meinPlanet;
PImage meinNebel;
// Fluggeschwindigkeit deklarieren und initialisieren
float v = 4;
// Startpositionen der Objekte deklarieren und initialisieren
float xPlanet = 40;
float yPlanet = 0;
float xNebel = 120;
float yNebel = 35;
void setup() {
size(280, 280);
smooth();
xRaumschiff = width/2;
// Ursprung für die Anzeige von Bildern ins Zentrum des Bildes setzen
imageMode(CENTER);
// Bilder in die bereit gestellten Variabeln einmalig !!! laden
meinPlanet = loadImage("planet.png");
meinNebel = loadImage("nebel.png");
}
void draw() {
background(150);
if (gestartet == false) {
fill(255);
text("'s' für Start", 10, 20);
text("bewegen mit den Pfeiltasten links | rechts", 10, 40);
}
else {
// Planet bewegen und allenfalls an oberen Rand mit zufälliger xPosition setzen
yPlanet = yPlanet + v;
if (yPlanet > height) {
yPlanet = 0;
xPlanet = random(0,width);
}
// Nebel bewegen und allenfalls an oberen Rand mit zufälliger xPosition setzen
yNebel = yNebel + v;
if (yNebel > height) {
yNebel = 0;
xNebel = random(0, width);
}
// Bilder an der aktuellen Position anzeigen
image(meinPlanet,xPlanet,yPlanet);
image(meinNebel,xNebel,yNebel);
}
// Raumschiff an der aktuellen Position anzeigen
raumschiffZeichnen(xRaumschiff, height-25);
}
// benutzerdefinierte Funktion zum Zeichnen eines Raumschiffs
void raumschiffZeichnen(int xPos, int yPos) {
translate(xPos, yPos); // Zeichnenursprung verschieben
fill(57, 63, 170);
noStroke();
arc(0, 0, 20, 60, PI, TWO_PI);
rect(-10, 0, 20, 10);
fill(183, 187, 242);
arc(0, -10, 10, 30, PI, TWO_PI);
fill(222, 58, 118);
arc(-10, 20, 10, 50, PI, PI+ HALF_PI);
arc(10, 20, 10, 50, PI+ HALF_PI, TWO_PI);
translate(-xPos, yPos); // Zeichnenursprung zurück verschieben
}
// Steuerung des Raumschiffs per Key-Ereignisse
void keyPressed() {
if (key == 's' || key == 'S') {
gestartet = true;
}
if (gestartet == true) {
if (keyCode == LEFT) {
xRaumschiff = xRaumschiff - schritt;
if (xRaumschiff < 0) {
xRaumschiff = width;
}
}
if (keyCode == RIGHT) {
xRaumschiff = xRaumschiff + schritt;
if (xRaumschiff > width) {
xRaumschiff = 0;
}
}
}
}
✎ Erweiterung 3:
Nun soll das einfache Spiel fertig gestellt werden:
- Führen Sie eine Variable
scorezum Zählen der Punkte ein. - Überwachen Sie mit der Funktion
dist(x1,y1,x2,y2)die Kollision des Raumschiffs mit dem Planet und dem Nebel. Eine Kollision mit dem Planet gibt 20 Punkte Abzug. Der Nebel enthält Energie und der Spieler erhält 10 Punkte gutgeschrieben.
Tipp: folgende Skizze zeigt die Idee zum Einsatz der Funktiondist():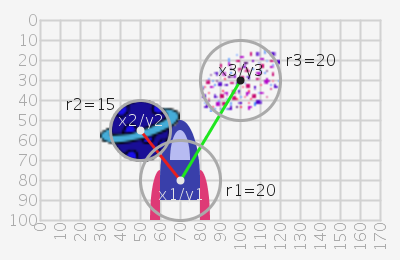
- Zeigen Sie den Score oben rechts an.
- Option: beschleunigen Sie das Spiel mit zunehmendem Score.
- Option: Starten Sie das Spiel neu, sofern der Score unter 0 fällt.
Lösungshinweis zu Aufgabe 2
Wenn die Distanz kleiner als die Summe der beiden Radien ist, so sind sich die Objekte zu nahe. Für Planet und Raumschiff beträgt die Summe der Radien z.B. 35. In code umgesetzt:if (dist(xPlanet, yPlanet, xRaumschiff, yRaumschiff) < 35) { ... }
So könnte die Lösung ticken - bitte antesten:
Lösung Erweiterung 3
int schritt = 6;
int xRaumschiff;
int yRaumschiff;
boolean gestartet = false;
// Variablen für die beiden Bilder deklarieren
PImage meinPlanet;
PImage meinNebel;
// Fluggeschwindigkeit deklarieren und initialisieren
float v = 4;
// Startpositionen der Objekte deklarieren und initialisieren
float xPlanet = 40;
float yPlanet = 0;
float xNebel = 120;
float yNebel = 35;
int score = 0;
void setup() {
size(280, 280);
smooth();
xRaumschiff = width/2;
yRaumschiff = height-25;
// Ursprung für die Anzeige von Bildern ins Zentrum des Bildes setzen
imageMode(CENTER);
// Bilder in die bereit gestellten Variabeln einmalig !!! laden
meinPlanet = loadImage("planet.png");
meinNebel = loadImage("nebel.png");
}
void draw() {
background(150);
if (gestartet == false) {
fill(255);
textSize(12);
textAlign(LEFT);
text("'s' für Start", 10, 20);
text("bewegen mit den Pfeiltasten links | rechts", 10, 40);
}
else {
// Planet bewegen
yPlanet = yPlanet + v;
// falls Kollision mit Raumschiff Punkte abziehen und zurück an oberen Rand
if (dist(xPlanet, yPlanet, xRaumschiff, yRaumschiff) < 35) {
yPlanet = 0;
xPlanet = random(0, width);
score = score - 20;
// falls Score kleiner 0 Spiel zurücksetzen
if (score < 0) {
score = 0;
gestartet = false;
yPlanet = 0;
yNebel = 0;
}
}
// falls Planet unten verschwunden an oberen Rand mit zufälliger xPosition setzen
if (yPlanet > height) {
yPlanet = 0;
xPlanet = random(0, width);
}
// Nebel bewegen
yNebel = yNebel + v;
// falls Kollision mit Raumschiff Punkte abziehen und zurück an oberen Rand
if (dist(xNebel, yNebel, xRaumschiff, yRaumschiff) < 45) {
yNebel = 0;
xNebel = random(0, width);
score = score + 10;
}
// falls Nebel unten verschwunden an oberen Rand mit zufälliger xPosition setzen
if (yNebel > height) {
yNebel = 0;
xNebel = random(0, width);
}
// Bilder an der aktuellen Position anzeigen
image(meinPlanet, xPlanet, yPlanet);
image(meinNebel, xNebel, yNebel);
// Score anzeigen
textSize(20);
textAlign(RIGHT);
text("Score: "+score, width-20, 20);
}
// Raumschiff an der aktuellen Position anzeigen
raumschiffZeichnen(xRaumschiff, yRaumschiff);
}
// benutzerdefinierte Funktion zum Zeichnen eines Raumschiffs
void raumschiffZeichnen(int xPos, int yPos) {
translate(xPos, yPos); // Zeichnenursprung verschieben
fill(57, 63, 170);
noStroke();
arc(0, 0, 20, 60, PI, TWO_PI);
rect(-10, 0, 20, 10);
fill(183, 187, 242);
arc(0, -10, 10, 30, PI, TWO_PI);
fill(222, 58, 118);
arc(-10, 20, 10, 50, PI, PI+ HALF_PI);
arc(10, 20, 10, 50, PI+ HALF_PI, TWO_PI);
translate(-xPos, yPos); // Zeichnenursprung zurück verschieben
}
// Steuerung des Raumschiffs per Key-Ereignisse
void keyPressed() {
if (key == 's' || key == 'S') {
gestartet = true;
}
if (gestartet == true) {
if (keyCode == LEFT) {
xRaumschiff = xRaumschiff - schritt;
if (xRaumschiff < 0) {
xRaumschiff = width;
}
}
if (keyCode == RIGHT) {
xRaumschiff = xRaumschiff + schritt;
if (xRaumschiff > width) {
xRaumschiff = 0;
}
}
}
}
Einstieg
Der folgende Code erstellt untenstehende Grafik. Es fällt auf, dass im Code die line()-Anweisung wiederholt eingesetzt wird.
size(330, 100); background(230); smooth(); stroke(0,0,200); strokeWeight(6); line(10, 20, 60, 80); line(70, 20, 120, 80); line(130, 20, 180, 80); line(190, 20, 240, 80); line(250, 20, 300, 80);

Wiederholungen lassen sich oft mit Schleifen vereinfachen. Obiger Code kann wie folgt charakterisiert werden:
- es sind 5 Wiederholungen,
- die Linien starten alle mit y-Koordinate 20 und
- enden bei y-Koordinate 80,
- die Linien haben in x-Richtung eine konstante Spannweite von 50 Pixel,
- die kleinste x1-Koordinate ist 10, die grösste 250,
- die kleinste x2-Koordinate ist 70, die grösste 310.
Für diese Anwendung eignet sich eine Zählerschleife, die sogenannte for-Schleife:
for (int i=10; i <= 250; i=i+60) {
line(i, 20, i+50, 80);
}
✎ Aufgaben:
- Übernehmen Sie die erste Version des Codes und ersetzen Sie die fünf
line()-Anweisungen durch diefor-Schleife. - Wo finden sich die festgestellten Eigenschaftenin in der
for-Anweisung? - x1-Koordinate variiert von 10 bis 250 Pixel,
- x-Spannweite 50 Pixel,
- y1 ist fix 20 Pixel und y2 ist fix 80 Pixel,
- 5 Wiederholungen.
Man kann alle Eigenschaften mit Ausnahme der 5 Wiederholungen erkennen. In der folgenden Variante lässt sich die Anzahl Wiederholungen besser erkennen, dafür andere Eigenschaften schlechter:
for (int i=0; i <5; i=i+1) {
line(10+i*60, 20, 10+i*60+50, 80);
}
Zählerschleife: for( ) { }
Bei der Zählerschleife steht die Anzahl Wiederholungen zu Beginn der Schleife fest. Die Anweisung hat folgende Struktur: for(Initialisierung; Bedingung; Update). Konkret sieht die dreigliedrige Anweisung wie folgt aus:
for (int i=0; i <10; i=i+1) {
line(10+i*30, 20, 10+i*30, 80);
}
Die Zählervariable i wird deklariert und mit 0 initialisiert. Als Bedingung wird i muss kleiner 10 sein festgelegt. Und am Ende jedes Schleifendurchgangs wird i zu i + 1. Die Zählvariable wird also mit 0 startend hochgezählt über 1, 2, ... bis 9. Am Schluss wird sie gar auf 10 erhöht, wobei i dann die Bedingung nicht mehr erfüllt und der Programmlauf dem false-Pfad im Flussdiagramm folgt. D.h. die Schleife wird beendet (vgl. Abb.).
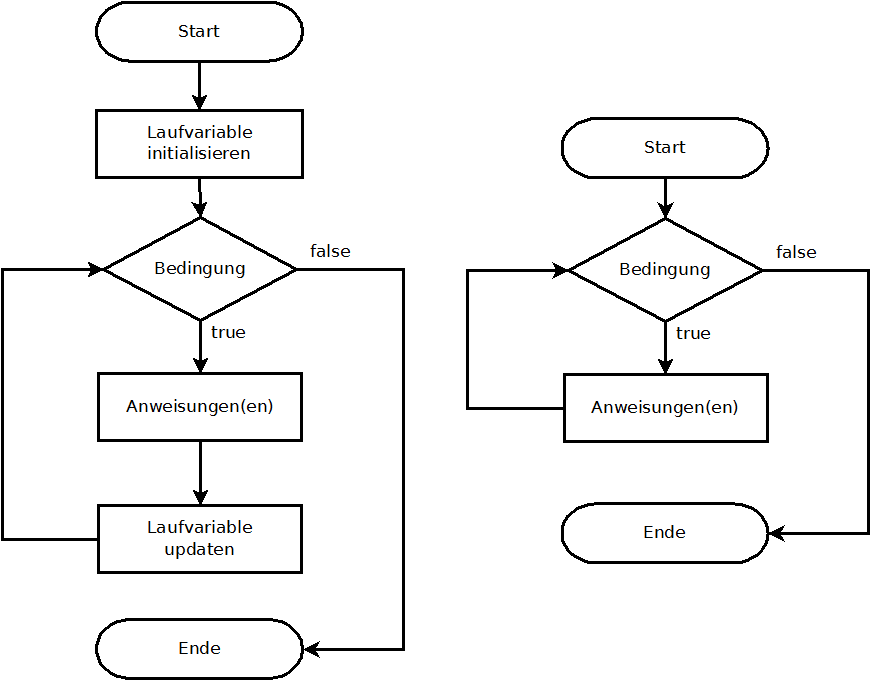
Die oben in Codeform präsentierte for-Schleife generiert folgende Grafik:

✎ Aufgaben:
- Verändern Sie die oben als Code gezeigte
for-Schleife so, dass folgende zwei Varianten entstehen. Speichern Sie die einzelnen Sketches. - Tipp zur 2. Variante: es sind zwei Anweisungen innerhalb der Schleife notwendig.


Lösung Variante 1.
size(330, 100);
background(230);
smooth();
stroke(0,0,200);
strokeWeight(4);
for (int i=0; i <10; i=i+1) {
line(10+i*30, 20, 10+i*30+30, 80);
}
Lösung Variante 2.
size(330, 100);
background(230);
smooth();
stroke(0,0,200);
strokeWeight(4);
for (int i=0; i <10; i=i+1) {
line(10+i*30, 20, 10+i*30+30, 50);
line(10+i*30+30, 50, 10+i*30, 80);
}
✎ Übungen
Festigen Sie die Anwendung der for-Schleife indem Sie folgende sechs Beispiele selber programmieren. Analysieren Sie dazu jede der 200*200 Pixel grossen Abbildungen:
- Welche Form kommt zum Einsatz?
- Wie viele Wiederholungen sind erkennbar?
- In welchem Wertebereich verändern sich die einzelnen Koordinaten x1, width etc.?
- Welche Koordinaten bleiben fix, z.B. y2?
- etc.
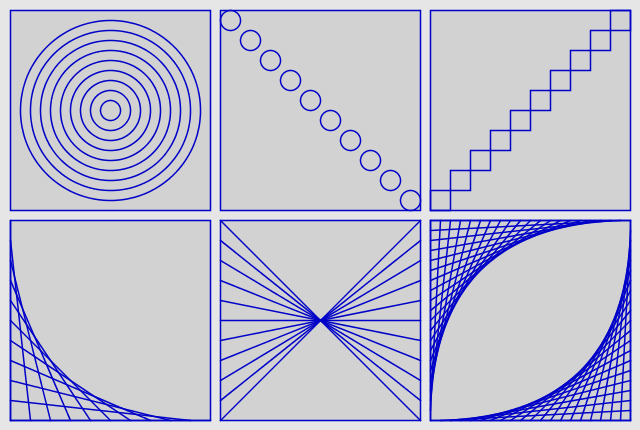
Lösung oben links
for (int i=0; i<10; i=i+1) {
ellipse(100,100,i*20, i*20);
}
Lösung oben mitte
for (int i=0; i<10; i=i+1) {
ellipse(i*20+10, i*20+10, 20, 20);
}
Lösung oben rechts
for (int i=0; i<10; i=i+1) {
rect(i*20, 180-i*20, 20, 20);
}
Lösung unten links
for (int i=0; i<11; i=i+1) {
line(0, i*20, i*20, 200);
}
Lösung unten mitte
for (int i=0; i<11; i=i+1) {
line(0, i*20, 200, 200-i*20);
}
Lösung unten rechts
for (int i=0; i<21; i=i+1) {
line(0, 200-i*10, i*10, 0);
line(200, i*10, 200-i*10, 200);
}
Schleife mit Bedingung zu Beginn: while( ) { }
Bei der while-Schleife ist zu Beginn unbekannt, wie oft sie durchlaufen wird. Da die Bedingung zu Beginn der Schleife steht, wird sie nie, einmal oder mehrmals durchlaufen.
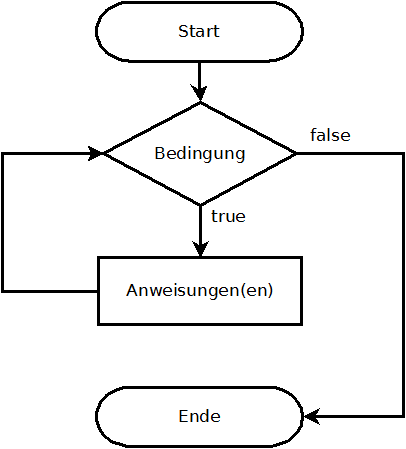
float a = 1;
while(a < 100) {
ellipse(10+3*a,50,a,a);
a = a*1.2;
}
Schleife mit Bedingung am Schluss: do { } while( )
Bei der do while-Schleife ist zu Beginn unbekannt, wie oft sie durchlaufen wird. Da die Bedingung zum Schluss steht, wird sie mindestens einmal durchlaufen.
Die allgemeine Syntax ist:
int a = 1;
do {
a = a + 1;
} while (a < 13);
Eine sinnvolle Anwendung wäre beim euklidischen Algorithmus zur Berechnung des ggT (grösster gemeinsamer Teiler).

✎ Aufgabe:
- A: Programmieren Sie den euklidischen Algorithmus mit Hilfe der
do while-Schleife und der Rest-Division%. Processing-Referenz zur Restdivision (Modulo-Division). - B: Erweitern Sie das Programm aus A so, dass in der Konsole die folgende Ausgabe resultiert:
Der ggT von a=252 und b=196 ist gleich 28.
Lösung A
int a = 252;
int b = 196;
int rest;
do {
rest = a % b;
a = b;
b = rest;
} while (rest > 0);
println("Der ggT ist gleich "+a);
Lösung B
int a = 252;
int b = 196;
int a1 = a;
int b1 = b;
int rest;
do {
rest = a % b;
a = b;
b = rest;
} while (rest > 0);
println("Der ggT von a=" + a1 + " und b=" + b1 +" ist gleich " + a);
verschachtelte for-Schleifen
Ein zweidimensionales Array wie abgebildet darzustellen, geht am einfachsten mit einer verschachtelten for-Schleife:
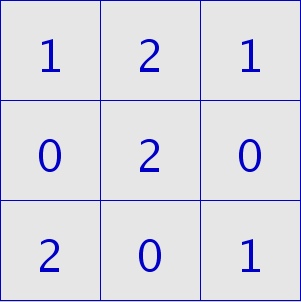
for(int i=0; i<3;i++) {
for(int j=0; j<3;j++) {
fill(230);
rect(i*s,j*s,s,s);
fill(0,0,200);
text(meinKoordinatenfeld[i][j],i*s+s/2,j*s+s/2);
}
}
Hinweis: verschachtelte for-Schleifen müssen unterschiedliche Zählvariabeln aufweisen. Im Beispiel sind dies i und j.
gesamter Code zum Array-Beispiel
// Deklaration
int[][] meinKoordinatenfeld;
// Initialisierung & Zuweisung kombiniert
meinKoordinatenfeld = new int[][] {{1, 0, 2},{2, 2 , 0},{1, 0, 1}};
size(301,302);
float s = 100;
textAlign(CENTER,CENTER);
textSize(45);
stroke(0,0,200);
for(int i=0; i<3;i++) {
for(int j=0; j<3;j++) {
fill(230);
rect(i*s,j*s,s,s);
fill(0,0,200);
text(meinKoordinatenfeld[i][j],i*s+s/2,j*s+s/2);
}
}
✎ Aufgabe 1
Die folgende Darstellung ist mit zwei for-Schleifen realisiert. Beantworten Sie folgende Fragen:
- Sind die
for-Schleifen verschachtelt oder nicht? Argumentieren Sie. - Warum ist der Kreis oben links anders gefärbt?
- Klappen Sie unten den Code auf und übernehmen Sie ihn in einen leeren Sketch. Experimentieren Sie durch Manipulation der Schleifen.

Code zum Experimentieren
size(660, 120);
background(230);
smooth();
noStroke();
fill(30,30,230,140);
for (int x = 0; x < width+45; x = x+40) {
ellipse(x, 0, 40, 40);
}
fill(230,30,30,140);
for (int y = 0; y < height+45; y = y+40) {
ellipse(0, y, 40, 40);
}
PS: Der Kreis oben links ist andersfarbig, weil zwei unterschiedliche Farben mit reduzierter Deckkraft übereinander liegen.
Verschachteln Sie die beiden for-Schleifen.

✎ Aufgabe 2
Programmieren Sie verschachtelte for-Schleifen so, dass folgende Darstellung entsteht. Tipps:
- Die Abbildung besteht aus lauter Rechtecke der Grösse 5*5 Pixel.
- Pro Spalte und pro Zeile sind es 51 Rechtecke. Die Fenstergrösse ist also 255*255 Pixel.
- Der Rot-Anteil der Farben ändert sich von links nach rechts von 0 auf 255.
- Der Blau-Anteil der Farben ändert sich von oben nach unten von 0 auf 255.

Lösung
size(255, 255);
smooth();
stroke(70);
for (int x = 0; x < 51; x = x+1) {
for (int y = 0; y < 51; y = y+1) {
fill(x*5,30,y*5);
rect(x*5, y*5, 5, 5);
}
}
PS: Die Rot- und Blau-Anteile der Farbwerte errechnen sich je aus einer Zählvariabel, hier x*5 bzw. y*5. Der Grünanteil ist in der Musterlösung zufällig auf 30 fixiert.
if-Anweisung
Die if-Anweisung verzweigt den Programmablauf. Wenn eine Bedingung wahr (true) ist, so werden die folgenden Anweisungen ausgeführt, sonst (false) werden diese übersprungen.
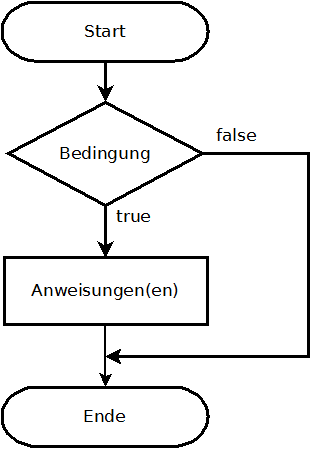
Die allgemeine Schreibweise ist:
if (Bedingung) {
Anweisung 1;
Anweisung 2;
...
Anweisung n;
}
✎ Aufgabe
Beobachten Sie obigen Sketch und ergänzen Sie folgenden Satz:
Wenn ........., dann ......... .
Lösung
Richtig! Wenn die x-Koordinate des Pacmans grösser als die Fensterbreite ist, dann wir sie auf 0 gesetzt. Die Fensterbreite ist in der Systemvariable width gespeichert.
if (xPos > width) {
xPos = 0;
}
✎ Anwendung
Programmieren Sie ebenfalls eine Form, die nach rechts wandert, und bevor sie rechts aus dem Fenster verschwindet an den linken Rand gesetzt wird.
Code Pacman-Beispiel
int xPos = 0;
int geschwindigkeit = 5;
void setup() {
size(660,100);
smooth();
}
void draw() {
background(230);
fill(0,0,200);
xPos = xPos + geschwindigkeit;
if (xPos > width) {
xPos = 0;
}
arc(xPos, height/2, 70, 70, PI/8, TWO_PI - PI/8);
}
if-else-Anweisung
Die if-else-Anweisung ermöglicht eine Wenn-Dann-Sonst Aussage. Wenn die Bedingung nicht erfüllt ist, werden alternative Anweisungen durchlaufen.
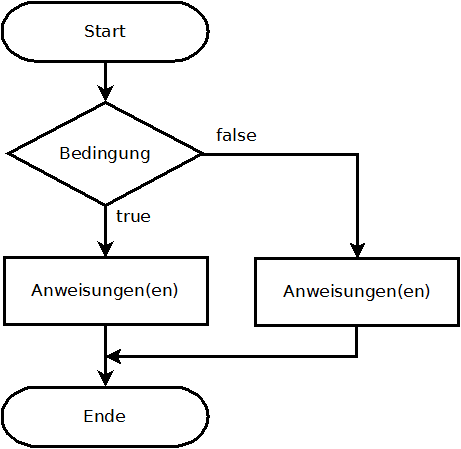
Die allgemeine Schreibweise ist:
if (Bedingung) {
Anweisung 1;
...
Anweisung n;
}
else {
Anweisung 1;
...
Anweisung n;
}
✎ Aufgabe
Bewegen Sie die Maus über obigem Sketch und ergänzen Sie folgenden Satz:
Wenn ........., dann ........., sonst ......... .
Lösung
Der Pacman wird abhängig von der y-Koordinaten der Maus gezeichnet. Ist die Systemvariable mouseY grösser als die Häfte der height-Systemvariable (Fensterhöhe), so schaut der Pacman nach unten, sonst nach oben.
Codeausschnitt:
if (mouseY > height/2) {
arc(xPos, height/2, 70, 70, HALF_PI + PI/8, TWO_PI + 3*PI/8);
}
else {
arc(xPos, height/2, 70, 70, PI + 5*PI/8, 3*PI + 3*PI/8);
}
✎ Anwendung
Setzen Sie diese Codezeilen in das voherige if-Beispiel ein.
Lösung
int xPos = 0;
int geschwindigkeit = 5;
void setup() {
size(660, 100);
smooth();
}
void draw() {
background(230);
fill(0, 0, 200);
xPos = xPos + geschwindigkeit;
if (xPos > width) {
xPos = 0;
}
if (mouseY > height/2) {
arc(xPos, height/2, 70, 70, HALF_PI + PI/8, TWO_PI + 3*PI/8);
}
else {
arc(xPos, height/2, 70, 70, PI + 5*PI/8, 3*PI + 3*PI/8);
}
}
if-else-if-Anweisung
Die if-else-if-Anweisung ermöglicht mehrere aufeinanderfolgende Bedingungen. Ist eine Bedingung wahr, werden die zugeordneten Anweisungend durchlaufen und anschliessend die if-else-if-Anweisung beendet. Nur bei false wird die nächste Bedingung getestet.
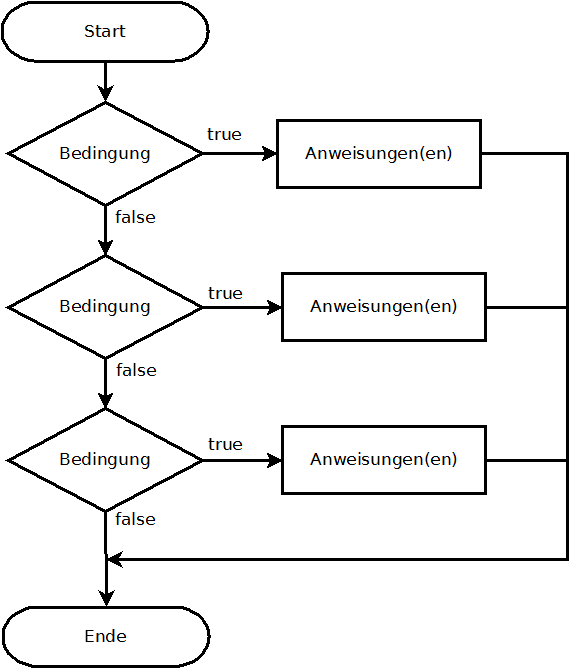
Die allgemeine Schreibweise ist:
if (Bedingung) {
Anweisung 1;
...
}
else if (Bedingung) {
Anweisung 1;
...
}
else if (Bedingung) {
Anweisung 1;
...
}
else {
Anweisung 1;
...
}
Es können beliebig viele else if Blöcke eingefügt werden.
✎ Aufgabe
Bewegen Sie die Maus über dem obigen Sketch in die drei Felder. Formulieren Sie nach dem Muster:
Wenn ........., dann ........., sonst falls ......... , sonst ......... .
Lösung
Wenn die Maus im ersten Drittel liegt, so bewegt sich der Pacmann nach links, sonst falls die Maus im mittleren Drittel liegt, steht er still und sonst bewegt sich der Pacman nach rechts.
Codeausschnitt:
if (mouseX < 220) {
geschwindigkeit = -5;
}
else if (mouseX < 440) {
geschwindigkeit = 0;
}
else {
geschwindigkeit = 5;
}
✎ Anwendung
Setzen Sie diesen Codeauschnitt in Ihren eigenen Sketch ein. So dass sich Ihre Form analog verhält. Variieren Sie die Grenzwerte.
Code Pacman-Beispiel
int xPos = 0;
int geschwindigkeit = 5;
void setup() {
size(660, 100);
smooth();
}
void draw() {
background(230);
fill(0, 0, 200);
if (mouseX < 220) {
geschwindigkeit = -5;
}
else if (mouseX < 440) {
geschwindigkeit = 0;
}
else {
geschwindigkeit = 5;
}
xPos = xPos + geschwindigkeit;
if (xPos > width) {
xPos = 0;
}
if (xPos < 0) {
xPos = width;
}
arc(xPos, height/2, 70, 70, PI/8, TWO_PI - PI/8);
}
switch-Anweisung
Die switch-Anweisung ermöglicht eine Mehrfachverzweigung abhängig vom Wert einer Variablen. Der Datentyp dieser Variable kann byte, char, short oder int sein.
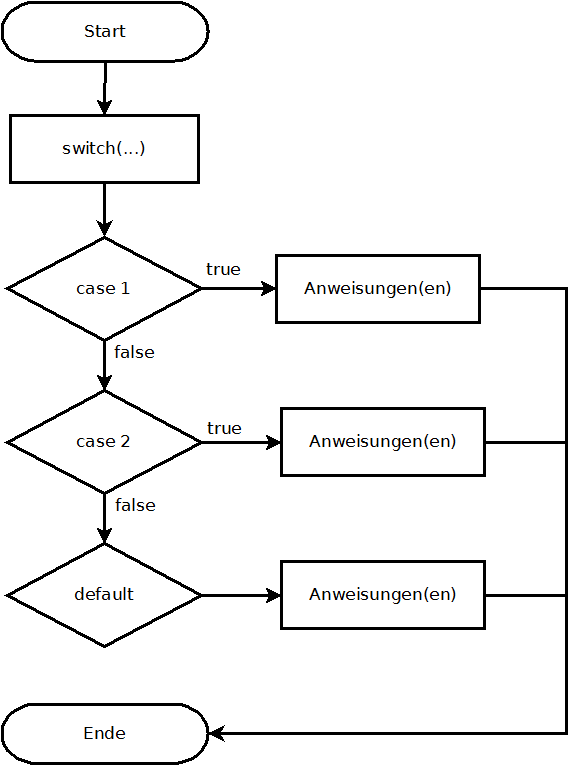
Die allgemeine Schreibweise ist:
switch (Variablenname) {
case KONSTANTE1:
Anweisung 1;
...
Anweisung n;
break;
case KONSTANTE2:
Anweisung 1;
...
Anweisung n;
break;
default:
Anweisung 1;
...
Anweisung n;
break;
}
Es können beliebig viele case-Abschnitte eingefügt werden. Der default-Abschnitt ist nicht zwingend.
✎ Aufgabe
Bewegen Sie die Maus über die Felder des obigen Sketch. Formulieren Sie, wie der Pacman reagiert.
Lösung
Je weiter rechts das berührte Feld, desto schneller bewegt sich der Pacman.
Im Code wird mit einer Division der x-Koordinate durch die Felbreite ermittelt, in welchem Feld die Maus sich befindet. Das Resultat der Division wird mit der int()-Funktion in eine Ganzzahl vom typ int umgerechnet. Das Ergebnis ist im Bereich [0..5] und wird in der Variable feldNr vom Datentyp int gespeichert. Diese Variable wird mit einer switch-Anweisung ausgewertet:
feldNr = int(mouseX / feldBreite);
switch (feldNr) {
case 0:
geschwindigkeit = 1;
break;
case 1:
geschwindigkeit = 3;
break;
case 2:
geschwindigkeit = 5;
break;
case 3:
geschwindigkeit = 7;
break;
case 4:
geschwindigkeit = 9;
break;
case 5:
geschwindigkeit = 11;
break;
default:
geschwindigkeit = 0;
}
✎ Anwendung
Bauen Sie eine ähnliche Geschwindigkeits-Steuerung in Ihren Sketch ein.
Code Pacman-Beispiel
int xPos = 0;
int geschwindigkeit = 5;
int feldBreite = 110;
int feldNr;
void setup() {
size(660, 100);
smooth();
}
void draw() {
background(230);
fill(0, 0, 200);
feldNr = int(mouseX / feldBreite);
switch (feldNr) {
case 0:
geschwindigkeit = 1;
break;
case 1:
geschwindigkeit = 3;
break;
case 2:
geschwindigkeit = 5;
break;
case 3:
geschwindigkeit = 7;
break;
case 4:
geschwindigkeit = 9;
break;
case 5:
geschwindigkeit = 11;
break;
default:
geschwindigkeit = 0;
}
xPos = xPos + geschwindigkeit;
if (xPos > width) {
xPos = 0;
}
arc(xPos, height/2, 70, 70, PI/8, TWO_PI - PI/8);
}
Abschluss-Übung
Schreiben Sie einen Sketch nach folgendem Vorbild:
Hinweise:
- Die Rechtecke werden mit Hilfe einer Schleife gezeichnet.
- Die Farbwerte sind in einem Array vom Typ
colorgespeichert. - Über welchem Farbfeld die Maus sich befindet wird berechnet.
- Wenn die Maus in der oberen Fensterhälfte ist, wird die entsprechende Farbe aus dem Array übernommen, sonst wird eine rote Standardfarbe verwendet.
Lösung
Kommentar zum Code
- In den Zeilen 8 bis 10 werden mit einer Schleife die Farbwerte für das Array berechnet. Genauer wird nur der Rotwert abhängig von
iberechnet. - Die Zeilen 19 bis 22 zeichnen die Rechtecke oben in der entsprechenden Farbe aus dem Array.
- Mit Hilfe einer
if-Verzweigung wird entschieden, ob die Farbe aus dem Array oder die rote Standardfarbe zur Anwendung kommt (s. Zeilen 24 bis 29).
int feldSeite= 60;
int anzFelder = 11;
int feldNr;
color[] feldFarben;
void setup() {
feldFarben = new color[anzFelder];
for (int i=0; i < anzFelder; i=i+1) {
feldFarben[i] = color(255-i*10, 200, 42);
}
size(660, 120);
smooth();
}
void draw() {
background(230);
stroke(210);
feldNr = int(mouseX / feldSeite);
for (int i=0; i < anzFelder; i=i+1) {
fill(feldFarben[i]);
rect(i*feldSeite, 0, feldSeite, feldSeite);
}
if (mouseY < height/2) {
fill(feldFarben[feldNr]);
}
else {
fill(180, 40, 40);
}
rect(0, 60, width, 60);
}