Suchen Sie möglichst schnell die angegebene CD in der Sammlung mit 128 Alben.
Wie viele Schritte brauchen Sie im Durchschnitt?
Lösungshinweise
Da die Sammlung nicht sortiert ist, muss man sie vollständig durchsuchen. Wenn man dies z.B. von links nach rechts macht, so stösst man im schlechtesten Fall erst an letzter Stelle auf das gesuchte Album. Es könnte aber auch sein, dass es bereits die erste CD ist. Im Durchschnitt muss man die Hälfte der Alben durchsuchen, hier 64 Stück. Der Aufwand der linearen Suche, auch sequenzielle Suche genannt, ist proportional mit der Anzahl Objekte. D.h. wenn es doppelt so viele Alben hat, muss man doppelt so lange suchen.
Die lineare Suche hat also eine Komplexität von O(n/2). » O-Notation
Suchen Sie wiederum möglichst schnell die angegebene CD in der Sammlung mit 128 Alben.
Wie sieht ein optimales Vorgehen aus?
Lösungshinweise
Die Sammlung ist alphabetisch sortiert und lässt einem das gesuchte Album schnell finden, da man feststellen kann, ob der gesuchte Eintrag weiter vorne oder weiter hinten zu finden ist. Dieses Verfahren lässt sich systematisieren:
- Nimm das mittlere Element.
- Ist dieses Element das gesuchte, so ist die Suche erfolgreich beendet.
- Ist dieses Element das einzig verbliebene, so ist die Suche erfolglos beendet.
- Ist das gefundene Element grösser als das gesuchte, so fahre mit Schritt i. für die linke Hälfte, sonst für die rechte Hälfte weiter.
Bei einer Sammlung von 128 Elementen zeigt die folgende Grafik ein möglicher Weg der wiederholten Halbierung:
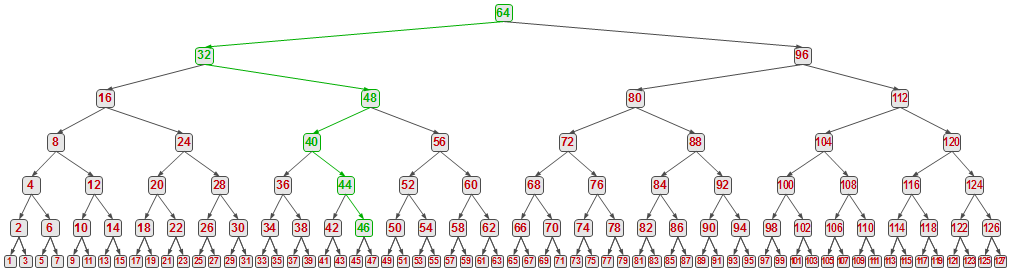
Im Extremfall bleibt am Schluss genau ein Album übrig. Entweder ist dieses das gesuchte oder die gesuchte CD kommt in der Sammlung nicht vor.
Das binäre Suchverfahren nimmt auf sich selbst Bezug (vgl. Punkt iv.) und ist folglich rekursiv. Zudem weist dieses Verfahren dank der fortschreitenden Halbierung der Suchbreite mit O(log2(n)) eine grosse Effizient auf. Dies zeigt auch die folgende Tabelle. » O-Notation
| Anzahl Objekte | Anzahl Halbierungen |
|---|---|
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 16 | 4 |
| 32 | 5 |
| 64 | 6 |
| 128 | 7 |
| 256 | 8 |
| 512 | 9 |
| 1'024 | 10 |
| 1'048'576 | 20 |
| 1'073'741'824 | 30 |
Die O-Notation gibt die Anzahl der Elementarschritte in Abhängigkeit von der Anzahl der Eingangbedaten an. In der Informatik spricht man von der Komplexität eines Problems. Man sagt „schwere Probleme“ wachsen exponentiell oder schneller und „leichte Probleme“ können mit einem maximal polynomiellen Verfahren (Algorithmus) gelöst werden.
| Komplexität | O-Notation | Kategorie | Beispiel |
|---|---|---|---|
| statisch | O(1) | leicht | |
| logarithmisch | O(log2(n)) | leicht | Binäre Suche |
| linear | O(n) | leicht | Lineare Suche |
| n log n | O(n * log2(n)) | leicht | Tournament-Sort, Merge-Sort, Quick-Sort |
| quadratisch | O(n2) | leicht | Bubble-Sort, Insertion-Sort |
| polynomiell | O(nk) für k > 2 | leicht | Dijkstra Algorithmus (Ameisen Algorithmus) |
| exponentiell | O(dn) für d > 1 | schwer | Fibonacci-Funktion rekursiv |
| faktoriell | O(n!) | schwer | Problem des Handelsreisenden (TSP Travelling Salesman Problem) |