Standort-Vektor
Jede Position kann als Vektor vom Ursprung zur Position definiert werden. Die Simulation zeigt dies im Koordinatensystem der Zeichenfläche. Hier nimmt die y-Koordinate von oben nach unten zu.
Hinweise: Den Punkt P können Sie verschieben.
Bewegungs-Vektor I
Jede Bewegung kann als Verschiebung von einem Punkt A zu einem Punkt B betrachtet werden. Diese Verschiebung wird als Vektor wie folgt notiert: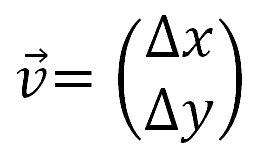 .
.
Hinweis: verschieben Sie mit der Maus die Punkte A und B.
Bewegungs-Vektor II
Bewegungen werden häufig mit einem Vektor abgebildet: 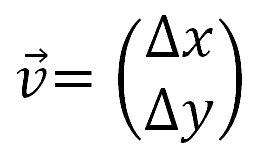 .
.
Die Simulation zeigt den Zusammenhang zu den Polarkoordinaten.
Hinweis: verändern Sie mit den Pfeiltasten den Vektor und mit Mausklicks die Anzeige.
Addition von Vektoren
Durch die Simulation erkennen wir, wie Vektoren v1 und v2 addiert werden: die beiden x-Komponenten und die beiden y-Komponenten werden separat addiert. Formal könnte man schreiben: v1.x + v2.x und v1.y + v2.y
Hinweis: die Punkte A bis C können mit der Maus bewegt werden und das Pluszeichen oben rechts verändert die Anzeige.
Subtraktion von Vektoren
Es zeigt sich, dass zwei Vektoren v1 und v2 wie folgt subtrahiert werden: v1.x - v2.x und v1.y - v2.y. Wie bei der Addition werden die x-Komponenten und die y-Komponenten separat verechnet. Der zweite Vektor wird mit *(-1) in seiner Richtung umgekehrt und zum ersten Vektor addiert.
Hinweis: die Punkte A bis C können mit der Maus bewegt werden, der Punkt C' hingegeben ist abhängig vom Standort Punkt C. Das blau hinterlegte Pluszeichen oben rechts verändert die Anzeige.
Vektoren mit Processing
In Processing steht die Klasse PVector für die Arbeit mit Vektoren zur Verfügung:

Basis-Methoden
- add() - addieren
- sub() - subtrahieren
- mult() - skalieren durch multiplizieren
- div() - skalieren durch dividieren
- mag() - Länge des Vektors berechnen
- setMag() - Länge des Vektors setzen
- normalize() - Länge des Vektors auf 1 normalisieren
- limit() - Länge des Vektors limitieren
weitere Methoden
- heading2D() - Richtung eines Vektors als Winkel
- rotate() - 2D Vektor um einen Winkel rotieren
- lerp() - lineare Interpolation zum zweitem Vektor
- dist() - euklidische Distanz zwischen zwei Vektoren
- angleBetween() - Winkel zwischen zwei Vektoren
- dot() - Skalar Produkt zweier Vektoren
- cross() - Kreuzprodukt zweier Vektoren
- random2D() - zufälliger 2D-Vektor
- random3D() - zufälliger 3D-Vektor
Weitere Details finden sich in der Referenz und der Lerneinheit von Daniel Shiffmann bei Processing.org.