Der Quicksort Algorithmus funktioniert nach dem "Teile und herrsche Prinzip". Dabei wird ein Problem solange in Teilprobleme zerlegt, bis diese einzeln gelöst - beherrscht - werden können. Durch die Lösung aller Teilprobleme, wird die Gesamtaufgabe gelöst.

Dies ausgewählte Karte dient als sogenanntes "Pivotelement". Alle Karten die kleiner als das Pivotelement sind, kommen in den linken Stapel und alle, die grösser sind, in den rechten Stapel. Liegen alle Karten einzeln vor, so sind die Karten von links nach rechts betrachtet aufsteigend sortiert.

Mit blauen Linien wird zum Schluss der sortierte Baum dargestellt. Da jeder Knoten maximal zwei Kindelemente hat, handelt es sich um einen binären Baum. Um die sortierten Karten auszulesen, wird der Baum gemäss dem Inorder-Verfahren durchlaufen. Beim Inorder-Verfahren, wird zuerst der linke Teilbaum, dann die Wurzel und schliesslich der rechte Teilbaum ausgegeben.
Beim folgenden Baum lautet die Inorder-Ausgabe: 1, 3, 4, 5, 8, 9, 12, 17, 19, 26, 30.

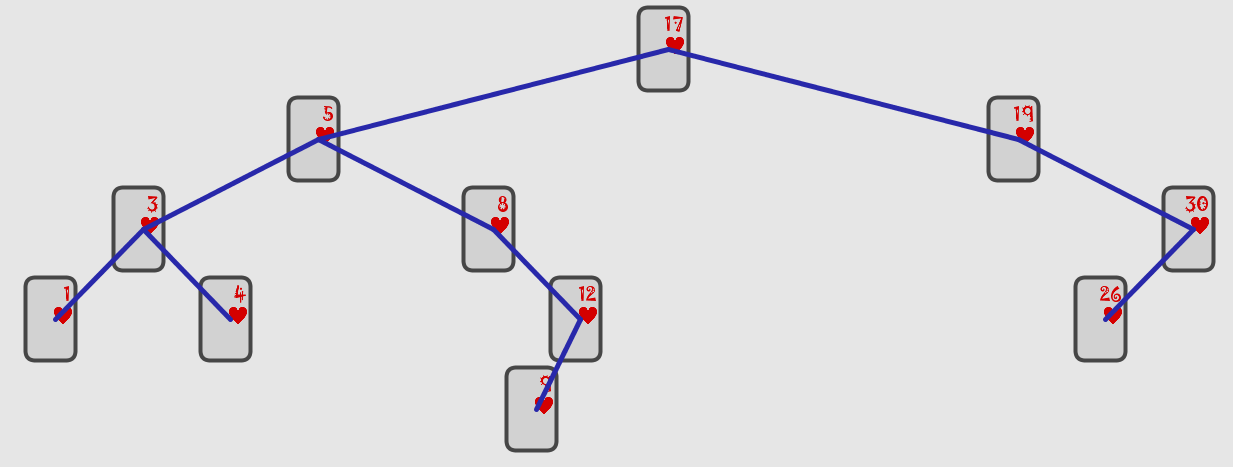
Beim Preorder-Verfahren wird die Wurzel zuerst ausgegeben und dann der linke und dann der rechte Teilbaum. Es folgt aus dem Baum die folgende Elementreihe: 17, 5, 3, 1, 4, 8, 12, 9, 19, 30, 26.

Beim Postorder-Verfahren, wird zuerst der linke und dann der rechte Teilbaum ausgegeben und schliesslich die Wurzel. Aus dem Beispiel ergibt sich die Reihe: 1, 4, 3, 9, 12, 8, 5, 26, 30, 19, 17

Dank des Teile und herrsche Prinzips ist der Quicksort Algorithmus sehr effizient und gehört zur Komplexitätsklasse "logarithmisch": O(log₂(n)).