Erdanziehung
Ein Objekt im freien Fall wird durch die Erdanziehung beschleunigt. Die Normfallbeschleunigung auf der Erde beträgt: gn = 9.80665 m/s2.
Hinweis: Neustart mit Mausklick oder Touch.
Aufgabe
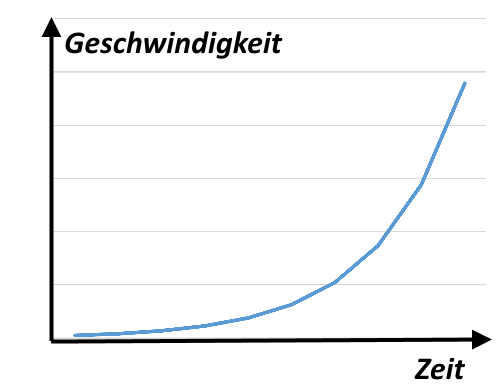
Wie beschleunigt sich das Objekt genau?
Lösungshinweis
Die Beschleunigung ist permanent und konstant. Die Geschwindigkeit des Objekts nimmt stetig zu. Sie wächst quadratisch.
Wurfbewegung
Wird ein Hilfspaket von einem Flugzeug aus abgeworfen, so zeigt sein Bewegungspfad diese typische Form.
Hinweis: Neustart mit Mausklick oder Touch.
Aufgabe
Analysieren Sie die Bewegung des abgeworfenen Pakets genau. Aus welchen Komponenten setzt sich diese zusammen?
Lösungshinweis
Das Paket hält die Geschwindigkeit des abwerfenden Flugzeuges als horizontale Bewegungskomponente bei (vgl. grüner Pfeil).
Ab dem Zeitpunkt des Abwurfes unterliegt das Paket der Erdanziehung. Diese beschleunigt das Paket permanent und konstant. Die entsprechende Bewegungskomponente nimmt mit der Zeit zu (vgl. blauer Pfeil).
Aus den beiden Bewegungsvektoren (-komponenten) resultiert durch Addition die Gesamtbewegung (schwarzer Pfeil) .
Die Addition von Vektoren ist in dieser separaten Simulation dargestellt.

Schweben
In der Simulation kann ein frei fallendes Objekt dank Antrieb gegen oben beschleunigt werden. Können Sie das Objekt in der Schwebe halten?
Hinweis: Neustart mit Mausklick oder Touch. Mausklick oder Pfeiltaste nach oben betätigt den Antrieb.
Aufgabe
Was passiert, wenn das Objekt oben aus dem Gesichtsfeld entschwindet?
Lösungshinweis
Mit dem Verschwinden am oberen Rand ist keine Beschleunigung durch Antrieb mehr möglich. Die Erdanziehung beschleunigt das Objekt ab dann alleine und führt dazu, dass es nach einiger Zeit wieder erscheint.
Fahrzeug
Die Simulation zeigt eine einfache Lenkung eines Objektes.
Hinweis: Lenkung mit den Pfeiltasten links | rechts und Gaspedal mit Pfeiltasten oben | unten.
Swipes in die entsprechende Richtung haben die gleiche Funktion.
Aufgabe
Welche Parameter braucht es für eine Lenkung?
Lösungshinweis
Eine Lekung kann ganz unterschiedlich umgesetzt werden. In diesem Beispiel wurden die folgenden Parameter verwendet:
- Vektor für die aktuelle Position des Fahrzeuges.
- Variable für die Fahrrichtung des Fahrzeuges (Winkel).
- Variable für Position des Lenkrades (Winkel)
- Variable für die Position des Gaspedals
- Hilfsvektor für gerichtete Geschwindigkeit
Programmierung im Detail:
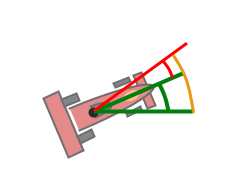
- Der mit dem Lenkrad eingeschlagene Winkel (rot) wird zum Richtungswinkel des Fahrzeugs (grün) addiert -> neuer Richtungswinkel (orange).
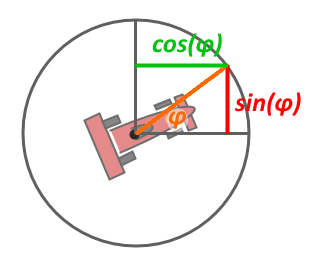
- Mit Hilfe des Einheitskreises werden aus dem Richtungswinkel (orange) die beiden Richtungskomponenten (x-Anteil grün, y-Anteil rot) für den Geschwindigkeitsvektors berechnet.
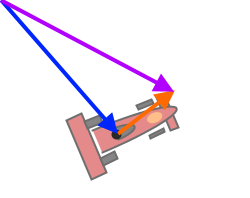
- Der Geschwindigkeitsvektor wird in Abhängigkeit vom Gaspedal mit
PVector.mult()auf die entsprechende Länge multipliziert. - Zum Schluss wird zum Positionsvektor (blau) des Fahrzeuges der Geschwindigkeitsvektor (orange) mit
PVector.add()addiert. Damit ist die neue Position (violett) des Wagens berechnet.
Zusätzlich braucht es noch eine Kalibrierung zwischen Einschlag der Lenkung und der Geschwindigkeit, damit die Bewegung des Fahrzeuges realistisch wirkt. Dazu eignet sich z.B. die Processing-Funktion map().
Einheitskreis und Polarkoordinaten werden mit mehreren Simulationen erklärt. Auch zum Thema Vektoren bestehen verschiedene Simulationen.