Coding'n Sim 4

Diese Seite hält Code und zusätzliche Hilfsmittel bereit.

Referenzlinks

Basiscode


// p5js Beispiel "Wolfram CA"
// https://p5js.org/examples/
// verändert sci

let w = 10;
let zellen;                                      // 1D-Array, wird mit Nullen und Einsen gefüllt
let generation = 0;
let regelset = [0, 1, 0, 1, 1, 0, 1, 0];         // 1D-Array zum Speichern des Regelsets, z.B. [0,1,1,0,1,1,0,1]

function setup() {
  createCanvas(640, 400);
  zellen = Array(floor(width / w));
  for (let i = 0; i < zellen.length; i++) {
    zellen[i] = 0;
  }
  // zum Start wird in der 0. Generation nur die mittlere Zelle auf Status "1" geseetzt
  zellen[zellen.length/2] = 1;
  
  background(245);
  frameRate(6);
}

function draw() {
  for (let i = 0; i < zellen.length; i++) {
    if (zellen[i] == 0)  {
      fill(50);
      noStroke();
      rect(i * w, generation * w, w, w);
    }
  }
  if (generation < height/w) {
    generieren();
  }
}

// generiert die nächste Generation
function generieren() {
  let nextgen = Array(zellen.length);
  // Für jede Zelle Status festlegen, aufgrund des Vorfahren und dessen Nachbarn.
  // Randzellen ignorieren, da diese nur einen Nachbarn haben.
  for (let i = 1; i < zellen.length-1; i++) {
    let links   = zellen[i-1];                   // Status des linken Nachbarn auslesen
    let ich     = zellen[i];                     // Status des Vorfahren auslesen
    let rechts  = zellen[i+1];                   // Status des rechten Nachbarns auslesen
    nextgen[i] = regeln(links, ich, rechts);     // neuer Status aufgrund dieser Dreiernachbarschaft bestimmen
  }
  // die aktuelle Generation (zellen) wird zur nächsten Generation (nextgen)
  zellen = nextgen;
  generation = generation + 1;
}

// Funktion enthält die Wolfram Regeln und liefert den passenden Wert zurück | umständlich programmiert - aber anschaulich
function regeln(a, b, c) {
  if (a == 1 && b == 1 && c == 1) {
    return regelset[0];
  }
  if (a == 1 && b == 1 && c == 0) {
    return regelset[1];
  }
  if (a == 1 && b == 0 && c == 1) {
    return regelset[2];
  }
  if (a == 1 && b == 0 && c == 0) {
    return regelset[3];
  }
  if (a == 0 && b == 1 && c == 1) {
    return regelset[4];
  }
  if (a == 0 && b == 1 && c == 0) {
    return regelset[5];
  }
  if (a == 0 && b == 0 && c == 1) {
    return regelset[6];
  }
  if (a == 0 && b == 0 && c == 0) {
    return regelset[7];
  }
  return 0;
}

Basiscode


// p5js Beispiel "Game of Life"
// https://p5js.org/examples/
// verändert sci

let w;
let spalten;
let zeilen;
let brett;
let next;

function setup() {
  frameRate(10);
  createCanvas(720, 400);
  w = 20;
  // Aanzahl Spalten und Zeilen berechnen
  spalten = floor(width / w);
  zeilen = floor(height / w);
  // schrullige Art 2D-Array in JS zu generieren
  brett = new Array(spalten);
  for (let i = 0; i < spalten; i++) {
    brett[i] = new Array(zeilen);
  }
  // dito., für ein zweites 2D-Array
  next = new Array(spalten);
  for (i = 0; i < spalten; i++) {
    next[i] = new Array(zeilen);
  }
  init();
}

function draw() {
  background(255);
  generieren();
  for ( let i = 0; i < spalten; i++) {
    for ( let j = 0; j < zeilen; j++) {
      if ((brett[i][j] == 1)) {
        fill(0);
      } else {
        fill(255);
      }
      stroke(0);
      rect(i * w, j * w, w-1, w-1);
    }
  }
}

// Brett bei Mausklick zurücksetzen
function mousePressed() {
  init();
}

// Brettzellen zufällig füllen
function init() {
  for (let i = 0; i < spalten; i++) {
    for (let j = 0; j < zeilen; j++) {
      // Randzellen mit Nullen füllen, die restlichen Zellen mit Zufallszahl [0, 1]
      if (i == 0 || j == 0 || i == spalten-1 || j == zeilen-1) {
        brett[i][j] = 0;
      } else {
        brett[i][j] = floor(random(2));
      }
      next[i][j] = 0;
    }
  }
}

// Neue Generation erstellen
function generieren() {

  // durch alle Zellen iterieren und direkte Nachbarn checken
  for (let x = 1; x < spalten - 1; x++) {
    for (let y = 1; y < zeilen - 1; y++) {
      // alle Werte des 3x3 Felder grossen Spots aufadieren
      let nachbarn = 0;
      for (let i = -1; i <= 1; i++) {
        for (let j = -1; j <= 1; j++) {
          nachbarn = nachbarn + brett[x+i][y+j];
        }
      }

      // kleiner Trick: Wert der zentralen Zelle subtrahieren, da in vorherige for-Schleife aufsummiert
      nachbarn = nachbarn - brett[x][y];
      // Überlebensregeln anwenden
      if ((brett[x][y] == 1) && (nachbarn <  2)) {                 // Einsamkeit
        next[x][y] = 0;
      } else if ((brett[x][y] == 1) && (nachbarn >  3)) {          // Überpopulation
        next[x][y] = 0;
      } else if ((brett[x][y] == 0) && (nachbarn == 3)) {          // Geburt
        next[x][y] = 1;
      } else {                                                     // Überleben
        next[x][y] = brett[x][y];                                  
      }
    }
  }

  // Swap! | Tausch!
  let temp = brett;
  brett = next;
  next = temp;
}

Basiscode


// Langton's Ant
// https://thecodingtrain.com/challenges/89-langtons-ant by D. Shiffman
// angepasst sci

let gitter;
let x;
let y;
let richtung;

let ANTNORD = 0;
let ANTOST = 1;
let ANTSUED = 2;
let ANTWEST = 3;

function setup() {
  createCanvas(400, 400);
  background(245);
  gitter = mache2DArray(width, height);
  x = width / 2;
  y = height / 2;
  richtung = ANTNORD;
}

function draw() {
  strokeWeight(1);
  for (let n = 0; n < 100; n++) {
    let status = gitter[x][y];
    if (status == 0) {
      dreheRechts();
      gitter[x][y] = 1;
    } else if (status == 1) {
      dreheLinks();
      gitter[x][y] = 0;
    }

    stroke(255);
    if (gitter[x][y] == 1) {
      stroke(0);
    }
    point(x, y);
    bewegeVorwaerts();
  }
}

function dreheRechts() {
  richtung++;
  if (richtung > ANTWEST) {
    richtung = ANTNORD;
  }
}

function dreheLinks() {
  richtung--;
  if (richtung < ANTNORD) {
    richtung = ANTWEST;
  }
}

function bewegeVorwaerts() {
  if (richtung == ANTNORD) {
    y--;
  } else if (richtung == ANTOST) {
    x++;
  } else if (richtung == ANTSUED) {
    y++;
  } else if (richtung == ANTWEST) {
    x--;
  }

  if (x > width - 1) {
    x = 0;
  } else if (x < 0) {
    x = width - 1;
  }
  if (y > height - 1) {
    y = 0;
  } else if (y < 0) {
    y = height - 1;
  }
}

function mache2DArray(spalten, zeilen) {
  let arr = new Array(spalten);
  for (let i = 0; i < arr.length; i++) {
    arr[i] = new Array(zeilen);
    for (let j = 0; j < arr[i].length; j++) {
      arr[i][j] = 0;
    }
  }
  return arr;
}

Referenzlinks

Braitenberg Vehikel ohne Sensorik, d.h. mit konstanter Geschwindigkeit:

Basiscode


// Braitenberg Basiscode

let posVehikel = 150;
let vVehikel = 3;
let rotWert;

function setup() {
  createCanvas(512, 200);
}

function draw() {
  background(240);
  for(let i =0;i<256;i=i+1) {
    stroke(i);
    line(i,0,i,height);
  }
  zeichneVehikel(posVehikel, height/2);
}

function zeichneVehikel(aktX, aktY) {
  translate(aktX-5, aktY);
  fill(255, 197, 47);
  strokeWeight(1);
  stroke(70);
  rect(-50, -20, 50, 40);
  fill(90);
  rect(-60, -30, 30, 10);
  rect(-60, 20, 30, 10);
  strokeWeight(3);
  noFill();
  arc(5, 0, 10, 10, 0.5*PI, 1.5*PI);
  line(-40, 0, 0, 0);
  line(-45, -20, -45, -5);
  line(-45, 5, -45, 20);
  arc(-40, -5, 10, 10, 0.5*PI, PI);
  arc(-40, 5, 10, 10, PI, 1.5*PI);
}

Referenzlinks

640'000 Berechnungsschritte in 320 Bildern im Zeitraffer:

Basiscode


// The Nature of Code by Daniel Shiffman
// https://natureofcode.com
// Kommentare und OOP adaptiert durch sci

let flock;

function setup() {
  createCanvas(640, 360);
  createP("Maus ziehen generiert zusätzliche Boids.");

  flock = new Flock();
  // zu Beginn ein Set von vierzig Boids generieren
  for (let i = 0; i < 40; i++) {
    let b = new Boid(width / 2, height / 2);
    flock.addBoid(b);
  }
}

function draw() {
  background(51);
  flock.run();
}

// neue Boids ergänzen
function mouseDragged() {
  flock.addBoid(new Boid(mouseX, mouseY));
}

// Schwarm Objekt
// macht wenig, managt nur das Array von allen Boids

class Flock {
  constructor() {
    this.boids = [];    // Array initialisieren
  }

  run() {
    for (let i = 0; i < this.boids.length; i++) {
      this.boids[i].run(this.boids);  // die ganze Boid-Liste an jeden Boid individuell übergeben
    }
  }

  addBoid(b) {
    this.boids.push(b);
  }
}


// Boid Klasse
// Methoden für Separation, Ausrichtung und Kohäsion

class Boid {
  constructor(x, y) {
    this.acceleration = createVector(0, 0);
    this.velocity = createVector(random(-1, 1), random(-1, 1));
    this.position = createVector(x, y);
    this.r = 3.0;
    this.maxspeed = 3;    // maximale Geschwindigkeit
    this.maxforce = 0.05; // maximale Steuerkraft
  }

  run(boids) {
    this.flock(boids);
    this.update();
    this.borders();
    this.render();
  }

  applyForce(force) {
    this.acceleration.add(force);
  }

  // wir errechnen jedes Mal eine neue Beschleunigung auf den drei Regeln basierend
  flock(boids) {
    let sep = this.separate(boids);   // Separation
    let ali = this.align(boids);      // Ausrichtung
    let coh = this.cohesion(boids);   // Kohäsion
    // zufällige Gewichtung der drei Regeln
    sep.mult(1.5);
    ali.mult(1.0);
    coh.mult(1.0);
    // die drei Kraftvektoren zur Beschleunigung addieren
    this.applyForce(sep);
    this.applyForce(ali);
    this.applyForce(coh);
  }

  // Methode zum Updaten der Position
  update() {
    // Geschwindigkeit updaten
    this.velocity.add(this.acceleration);
    // Geschwindigkeit begrenzen
    this.velocity.limit(this.maxspeed);
    this.position.add(this.velocity);
    // Beschleunigung nach jedem Durchgang auf 0 zurücksetzen
    this.acceleration.mult(0);
  }

  // eine Methode zur Berechnung und Anwendung einer Lenkkraft in Richtung eines Ziels
  seek(target) {
    let desired = p5.Vector.sub(target, this.position);  // ein Vektor der von der aktuellen Position zum Ziel zeigt
    // desired normalisieren und auf maximale Geschwindigkeit skalieren
    desired.normalize();
    desired.mult(this.maxspeed);
    // Steering = Desired minus Velocity
    let steer = p5.Vector.sub(desired, this.velocity);
    steer.limit(this.maxforce);  // auf maximale Steuerung limitieren
    return steer;
  }

  // zeichnet den Boid 
  render() {
    // ein Dreieck in die Bewegungsrichtung rotiert zeichnen
    let theta = this.velocity.heading() + radians(90);
    fill(127);
    stroke(200);
    push();
    translate(this.position.x, this.position.y);
    rotate(theta);
    beginShape();
    vertex(0, -this.r * 2);
    vertex(-this.r, this.r * 2);
    vertex(this.r, this.r * 2);
    endShape(CLOSE);
    pop();
  }

  // Begrenzungen rundum beachten
  borders() {
    if (this.position.x < -this.r)  this.position.x = width + this.r;
    if (this.position.y < -this.r)  this.position.y = height + this.r;
    if (this.position.x > width + this.r) this.position.x = -this.r;
    if (this.position.y > height + this.r) this.position.y = -this.r;
  }

  // Separation
  // Methode beachtet die nahen Boids und steuert weg
  separate(boids) {
    let desiredseparation = 25.0;
    let steer = createVector(0, 0);
    let count = 0;
    // Für jeden Boid im System checken, ob er zu nahe ist
    for (let i = 0; i < boids.length; i++) {
      let d = p5.Vector.dist(this.position, boids[i].position);
      // Ist die Distanz grösser als 0 und kleiner als gewünschter Abstand
      if ((d > 0) && (d < desiredseparation)) {
        // berechnet einen vom Nachbarn wegzeigenden Vektor
        let diff = p5.Vector.sub(this.position, boids[i].position);
        diff.normalize();
        diff.div(d);        // gewichtet durch die Distanz
        steer.add(diff);
        count++;            // zählen, wie viele Nachbarn zu nahe sind und berücksichtigt werden
      }
    }
    // Durchscnitt berechnen - dividiert durch die Anzahl
    if (count > 0) {
      steer.div(count);
    }

    // so lange der Vektor grösser als 0 ist
    if (steer.mag() > 0) {
      // implementiert gemäss Reynolds: Steuerung = Wunschrichtung - Geschwindigkeit
      steer.normalize();
      steer.mult(this.maxspeed);
      steer.sub(this.velocity);
      steer.limit(this.maxforce);
    }
    return steer;
  }

  // Ausrichtung
  // Für alle Boid des Systems die benachbart sind, die durchschnittliche Geschwindigkeit berechen
  align(boids) {
    let neighbordist = 50;
    let sum = createVector(0, 0);
    let count = 0;
    for (let i = 0; i < boids.length; i++) {
      let d = p5.Vector.dist(this.position, boids[i].position);
      if ((d > 0) && (d < neighbordist)) {
        sum.add(boids[i].velocity);
        count++;
      }
    }
    if (count > 0) {
      sum.div(count);
      sum.normalize();
      sum.mult(this.maxspeed);
      let steer = p5.Vector.sub(sum, this.velocity);
      steer.limit(this.maxforce);
      return steer;
    } else {
      return createVector(0, 0);
    }
  }

  // Kohäsion
  // Für die durchschnittliche Position (d. h. das Zentrum) aller in der Nähe befindlichen Boids wird der Steuerungsvektor in Richtung dieser Position berechnet
  cohesion(boids) {
    let neighbordist = 50;
    let sum = createVector(0, 0);   // mit einem leeren Vektor startend, alle Orte summieren
    let count = 0;
    for (let i = 0; i < boids.length; i++) {
      let d = p5.Vector.dist(this.position, boids[i].position);
      if ((d > 0) && (d < neighbordist)) {
        sum.add(boids[i].position); // Position addieren
        count++;
      }
    }
    if (count > 0) {
      sum.div(count);
      return this.seek(sum);  // zur Position hin steuern
    } else {
      return createVector(0, 0);
    }
  }
}

Basiscode


let myTable;
let maxRow;
let x;
let y;

function preload() {
  myTable = loadTable("data/test.csv", "csv", "header");
}

function setup() {
  createCanvas(500, 350);

  strokeWeight(4.5);
  maxRow = myTable.getRowCount();

  console.log(maxRow + " total Zeilen in Tabelle");
  background(30);

  stroke(210);
  let rows = myTable.getRows();
  for (let r = 0; r < rows.length; r++) {
    x = rows[r].getNum(0);
    y = rows[r].getNum(1);
    point(x - 400, 340 - y);
  }
}

Test Koordinaten


chX,chY
500,160
580,280
750,280
830,200
730,100
550,100
500,160

Klasse Pipe

class Pipe {
  constructor () {
    this.x = canvasWidth;
    this.y = 0;
    this.gap = random(gapMargin, canvasHeight - pipeGap - gapMargin);
  }
    //Röhre anzeigen
    show() {
        stroke(80,61,72);
        strokeWeight(3);
        fill(130,168,65);
        rect(this.x, this.y, pipeWidth, this.gap);
        rect(this.x,this.gap + pipeGap, pipeWidth, canvasHeight);
        
        //Röhre nach links bewegen
        this.x -= 2;
    }

    //Prüfung der Kollision der Röhre mit dem Vogel
    checkCollision(birdY) {

        //prüfe, ob der Vogel mit dem oberen Abschnitt der Röhre kollidiert
        if(collideRectCircle(this.x, this.y, pipeWidth, this.gap, birdX, birdY, birdSize)) {
            myScore.gameOver();
        }

        //prüfe, ob der Vogel mit dem unteren Abschnitt der Röhre kollidiert
        if(collideRectCircle(this.x,this.gap + pipeGap, pipeWidth, canvasHeight, birdX, birdY, birdSize)) {
            myScore.gameOver();
        }
    }
}

Klasse Score

class Score {
  constructor(score) {
    this.gameStatus = 0;
    this.actScore = 0;
    this.highScore = 0;
  }
  //Scoretext anzeigen
  show(scoreText) {
    textFont(scoreFont);
    textSize(canvasHeight/12);
    textAlign(CENTER);
    textStyle(BOLD);
    fill(255);
    stroke(0);
    strokeWeight(10);

    text(scoreText, 0, canvasHeight/10, canvasWidth, canvasHeight);
  }

  //Score erhöhen
  increase() {
    this.actScore++;
  }

  //der Vogel ist gestorben, das Spiel soll beendet werden
  gameOver() {
    this.gameStatus = 2;

    //neuer Highscore
    if (this.actScore > this.highScore) {
      this.highScore = this.actScore;
    }
  }
}

Basiscode


let r = 180;
let angle = 0;

function setup() {
  createCanvas(500, 500, WEBGL);
}

function draw() {
  orbitControl();
  background(51);
  rotateY(angle);
  angle = angle + 0.005;

  fill(200);
  stroke(150);

  sphere(r);

  // X-Achse rot anzeigen
  noStroke();
  fill(255, 0, 0);
  box(2.4 * r, 5, 5);
  push();
  translate(1.2 * r, 0, 0);
  box(10, 10, 10);
  pop();

  // Y-Achse grün anzeigen
  // ...
  
}

Texturbild

Das Bild ist auf den Nullmeridian ausgerichtet und einget sich optimal als p5js-Textur:

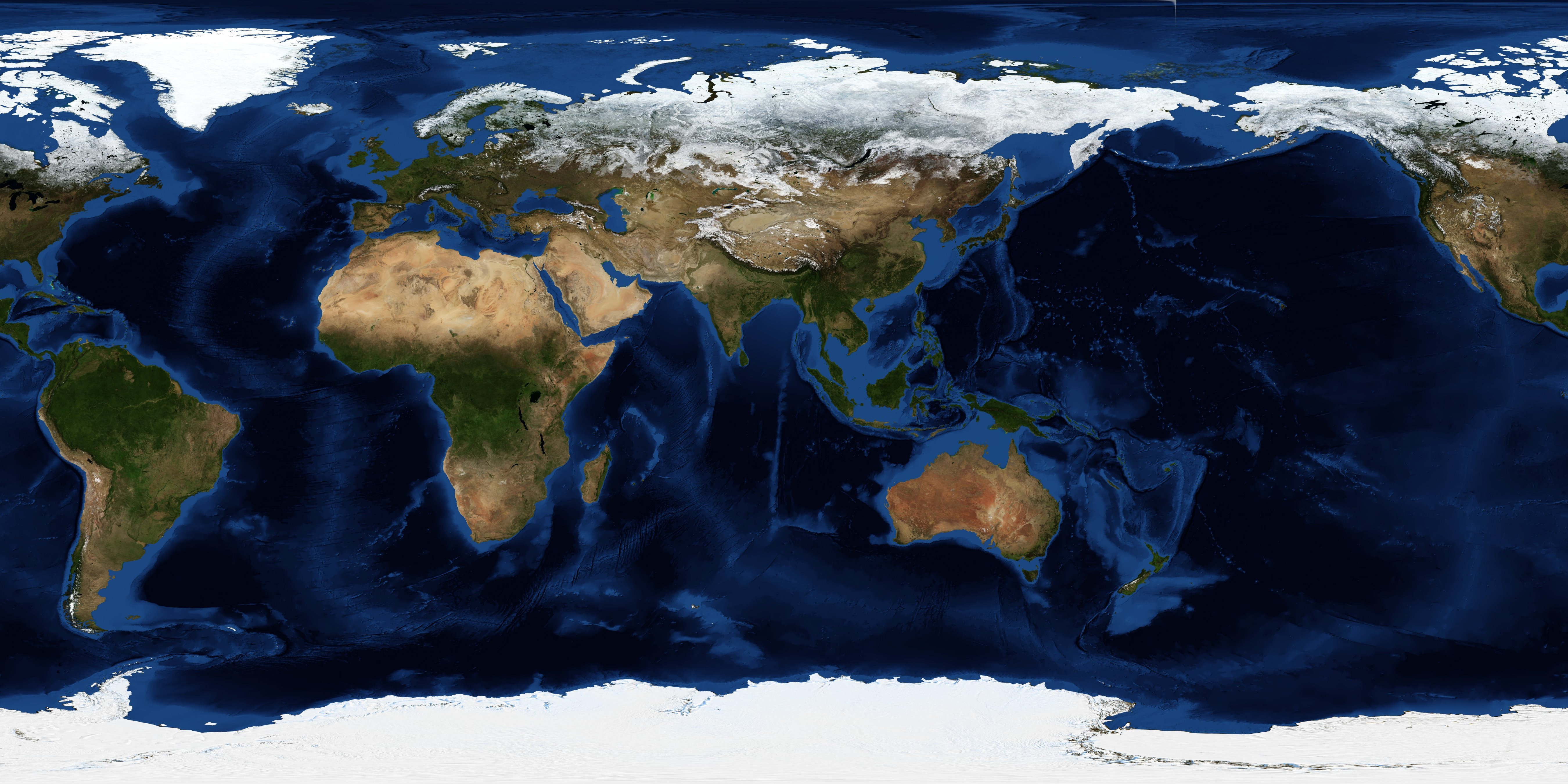
Realtime Erdbebendaten

Der US-amerikanische Erdbebendienst (USGS) liefert realtime Feeds in verschiedensten Formaten:

Links

fs in ksw